Deep Learning Specialization - Neural Networks and Deep Learning [2]
해당 내용은 Andrew Ng 교수님의 Coursera의 딥러닝 특화과정(Deep Learning Specialization)의 첫 번째 강의 Neural Networks and Deep Learning를 듣고 정리한 내용이다.
신경망 사고방식으로 기계 학습 문제를 설정하고 벡터화를 사용하여 모델 속도를 높여보자!
학습 목표
- Build a logistic regression model structured as a shallow neural network
- Build the general architecture of a learning algorithm, including parameter initialization, cost function and gradient calculation, and optimization implemetation (gradient descent)
- Implement computationally efficient and highly vectorized versions of models
- Compute derivatives for logistic regression, using a backpropagation mindset
- Use Numpy functions and Numpy matrix/vector operations
- Work with iPython Notebooks
- Implement vectorization across multiple training examples
- Explain the concept of broadcasting
얕은 신경망으로 구성된 로지스틱 회귀 모델 구축
매개변수 초기화, 비용 함수 및 기울기 계산, 최적화 구현(경사하강법)을 포함한 학습 알고리즘의 일반 아키텍처 구축
계산적으로 효율적이고 고도로 벡터화된 모델 버전 구현
역전파 사고방식을 사용하여 로지스틱 회귀에 대한 도함수를 계산
Numpy 함수 및 Numpy 행렬/벡터 연산 사용
iPython 노트북으로 작업
여러 훈련 예제에 걸쳐 벡터화 구현
개념 설명
Binary Classification

이진 분류 문제
입력이미지 : 고양이
출력 레이블: 고양이 일때 1 아니면 0
이미지를 저장하기위해 컴퓨터는 세개로 분리된 행렬 사용한다.
이미지가 64x64 이면 각각의 행렬도 64x64 사이즈가 된다.
입력 이미지는 빨간색, 녹색, 파란색 채널로 구성된 64x64 픽셀 이미지로 표현되며, 모든 픽셀의 채도값을 하나의 특징 벡터로 나타낸다.
특징벡터 x가 되고 이 이미지가 64x64 이면 벡터의 전체 차원은 64x64x3이 된다.
64x64x3=12288 , n(입력 특징 벡터의 차원)=nx=12288

이 강의에서 사용되는 표기법 정리
-훈련 데이터: (x, y) 쌍으로 표현
-x: x차원을 진 특징벡터
-y: 0 or 1 인 레이블
-훈련 데이터: m = m_train
예를 들어 첫 번째 훈련 예제는 (x1, y1)로 나타낼 수 있고, 마지막 훈련 예제는 (xm, ym)로 나타낼 수 있다.
-테스트 데이터 : m_test
입력 데이터를 다룰 때 대문자 X를 사용하여 입력값을 행렬로 표현합니다. 이 행렬은 입력 데이터 x1, x2, 등을 열로 쌓아서 만들어집니다. 이 행렬 X는 m개의 열을 가질 것이고 행은 nx개이다.
따라서 X는 nx x m 차원의 행렬이며, 파이썬에서 X.shape를 통해 이 형태를 확인할 수 있습니다.
출력 레이블 Y도 열 벡터로 표현되며, 대문자 Y로 나타냅니다. 예를 들어 Y1, Y2, 등으로 표현하며, 이는 1 x m 차원의 행렬을 의미합니다
Logistic Regression

로지스틱 회귀
: 로지스틱 회귀는 주로 이진 분류 문제를 다루는 지도 학습 알고리즘으로, 결과값 레이블 Y가 0 또는 1인 경우에 사용됩니다.
로지스틱 회귀에서 목표는 입력 특성 벡터 X를 고양이인지 아닌지를 판단하는 이진 분류 모델로 학습하는 것입니다. 이를 위해 결과값을 예측하는 데 Ŷ (Y hat)을 사용하며, Ŷ은 Y의 추정치를 나타냅니다. 이때, Ŷ이 1에 가까울수록 입력 이미지가 고양이일 확률이 높다고 판단합니다.
로지스틱 회귀의 모델은 입력값 X와 매개 변수인 W와 b로 정의되며, Ŷ을 생성하기 위해 입력값 X에 대한 선형 함수를 사용합니다.
그러나 이 함수의 결과값은 0과 1 사이에 있어야 하므로, 선형 함수의 출력을 확률로 변환하기 위해 시그모이드 함수를 사용합니다. 시그모이드 함수는 입력 Z를 받아 0에서 1 사이의 값을 출력합니다.
(로지스틱 회귀에서 목표는 매개 변수 W와 b를 학습하여 Ŷ이 Y가 1일 확률에 대한 좋은 추정치가 되도록 하는 것이다.)
그래프 설명
시그모이드 함수는 입력 Z에 대해 0과 1 사이의 값을 출력하는 함수로, 그래프는 Z가 증가함에 따라 부드럽게 0에서 1로 변화합니다.
시그모이드 함수 공식
시그모이드 함수의 공식은 다음과 같습니다: Z의 시그모이드 = 1 / (1 + e^(-Z)). 이때, Z가 매우 큰 양수일 때 시그모이드 함수의 값은 1에 가깝고, Z가 매우 작거나 음수일 때는 0에 가깝습니다.
(Z가 매우 큰값이면 e의 -z승은 0에 가까운 값임. z가 아주 큰 음수이면 e^-z는 매우 큰 값.)
로지스틱 회귀에서 매개 변수 W와 B를 학습하여 Ŷ이 Y가 1일 확률에 대한 좋은 추정치가 되도록 조정합니다.
신경망을 프로그래밍할 때, W와 B를 따로 다루는 표기법을 사용할 수 있으며, 추가 특성 X0을 정의하여 이를 1로 만들어주는 경우도 있습니다.여기선 쓰기 않는다.
-로지스틱 회귀(Logistic Regression) 정리-
로지스틱 회귀(Logistic Regression)는 주로 이진 분류(Binary Classification) 문제를 해결하는 데 사용되는 지도 학습 알고리즘 중 하나이다. 이 알고리즘은 입력 특성(Features)과 해당 입력이 특정 클래스에 속할 확률 사이의 관계를 모델링하는데 주로 쓰입니다.
이진 분류: 로지스틱 회귀는 입력 데이터를 두 개의 클래스 중 하나로 분류하는 문제를 해결합니다. 예를 들어, 메일이 "스팸" 또는 "스팸 아님" 중 어느 카테고리에 속하는지 예측하는 데 사용됩니다.
확률 모델: 로지스틱 회귀는 입력 특성과 클래스에 속할 확률 간의 관계를 나타내는 모델을 학습합니다. 이 모델은 입력 특성과 가중치(Weight) 벡터의 선형 조합을 시그모이드(Sigmoid) 함수에 적용하여 확률을 생성합니다.
시그모이드 함수: 로지스틱 회귀에서 시그모이드 함수는 입력값의 범위를 [0, 1]로 제한하는 역할을 합니다. 시그모이드 함수는 S 모양의 곡선을 가지며, 어떤 값에 대한 출력은 해당 값이 특정 클래스에 속할 확률로 해석됩니다.
학습과 최적화: 로지스틱 회귀는 학습 데이터를 사용하여 가중치와 바이어스(또는 편향)를 최적화하는 방식으로 훈련됩니다. 이때, 가중치와 바이어스는 손실 함수를 최소화하도록 조정됩니다. 주로 최대 우도 추정(Maximum Likelihood Estimation)을 사용하여 이를 수행합니다.
경계 결정: 로지스틱 회귀 모델은 입력 공간을 두 개의 클래스를 구분하는 결정 경계로 나타냅니다. 이 결정 경계는 시그모이드 함수의 출력이 0.5인 지점으로 정의되며, 이 지점을 기준으로 클래스를 분류합니다.
특성 선택과 정규화: 로지스틱 회귀에서는 모델의 성능을 향상시키기 위해 특성 선택(Feature Selection)과 정규화(Regularization) 기술을 사용할 수 있습니다.
Logistic Regression Cost Function


비용 함수(Cost Function)
출력인 Y hat은 W 전치 X에 시그모이드 함수를 적용한 것입니다.여기서 시그모이드 함수인 Z의 정의를 확인할 수 있습니다.

y hat은 위의 수식에서 정의된 대로 학습 예제 X에 대한 예측입니다. 각 학습 예제에 대해 다른 슈퍼스크립트를 사용하여 인덱싱합니다. 예를 들어, y hat I는 학습 예제 I에 대한 예측을 나타냅니다. 이는 시그모이드 함수를 사용하여 W 전치 X I (학습 예제의 입력)에 B를 더하여 얻습니다.

비용 함수 또는 오차 함수를 정의하여 모델의 출력인 y hat이 실제 레이블 y와 얼마나 일치하는지 측정할 수 있습니다. 제곱 오차를 사용할 수도 있지만, 로지스틱 회귀에서는 일반적으로 이것을 사용하지 않습니다. 왜냐하면 제곱 오차를 사용하면 최적화 문제가 비볼록(non-convex)하게 되어 여러 지역 최적점(local optima)이 있을 수 있어서 글레디언트 디센트(Gradient Descent)와 같은 최적화 알고리즘이 전역 최적점(global optimum)을 찾기 어려워집니다.
따라서 로지스틱 회귀에서는 다음과 같은 손실 함수를 사용합니다.

L(y hat, y) = -[y log(y hat) + (1 - y) log(1 - y hat)]

이 손실 함수는 다음과 같은 이유로 합리적인 선택입니다.
- y가 1인 경우, 손실 함수는 y hat에 대한 음의 로그 값을 최소화하려고 합니다. 따라서 y가 1이면 y hat을 가능한 크게 만들고자 합니다. 또한 y hat은 시그모이드 함수를 통과하기 때문에 1보다 크지 않습니다. 따라서 y가 1일 때, y hat을 1에 가깝게 만들려는 것입니다.
- y가 0인 경우, 손실 함수는 y hat에 대한 음의 로그 값 1 - y hat을 최소화하려고 합니다. 이것은 y가 0일 때 y hat을 가능한 작게 만들고자 합니다. 마찬가지로 y hat은 0에서 1 사이의 값이므로, y가 0일 때 y hat을 0에 가깝게 만들려는 것입니다.
이렇게 정의된 손실 함수는 각 학습 예제에 대해 얼마나 모델의 출력이 실제 레이블과 일치하는지를 측정하며, 전체 훈련 세트에 대한 비용 함수를 정의할 수 있습니다.

비용 함수란 머신 러닝 모델에서 사용되며 모델의 성능을 평가하고 모델의 매개변수를 최적화하는 데 사용되는 함수입니다. 로지스틱 회귀의 경우 비용 함수 J는 모델의 매개변수 W와 B에 적용되며 평균을 내는데, 이때 손실 함수의 각 훈련 예제에 적용됩니다. 손실 함수의 타입 m 중 하나가 각 훈련 예제에 적용됩니다.
로지스틱 회귀에서 사용되는 비용 함수 J는 다음과 같이 정의됩니다:
J(W, B) = (1/m)(-[y(i) log ŷ(i) + (1 - y(i)) log (1 - ŷ(i))])
여기서 각 항목을 설명하면:
J(W, B): 비용 함수. 모델의 매개변수 W와 B에 대한 비용입니다.
y(i): 실제 훈련 예제 i의 레이블 또는 타겟 값.
ŷ(i): 모델이 예측한 훈련 예제 i의 예측 값.
평균: 비용 함수를 모든 훈련 예제에 대해 평균을 내는 연산입니다.
비용 함수 J를 최소화하기 위해 모델은 학습 데이터에서 매개변수 W와 B를 조정하려고 시도합니다. 이 과정을 반복하여 모델을 훈련시킵니다.
요약하면, 비용 함수는 모델의 성능을 평가하고 매개변수를 조정하기 위한 핵심 요소이며, 로지스틱 회귀의 경우 로그 손실 함수를 사용하여 정의됩니다. 이 함수는 모델이 예측한 확률과 실제 레이블 간의 차이를 측정하고 최적화 과정에서 최소화됩니다.
- 손실 함수 (Loss Function): 손실 함수는 개별 훈련 예제에 대한 오류 또는 손실을 계산하는 함수입니다. 각 훈련 예제에 대해 모델의 예측값과 실제 레이블 간의 차이를 측정하며 개별 데이터 포인트에서 발생한 오류를 측정합니다.
- 비용 함수 (Cost Function): 비용 함수는 전체 훈련 세트에 대한 손실 함수의 평균입니다. 모든 훈련 예제에 대한 손실 값을 합산하고 그 값을 훈련 예제의 총 수로 나누어 계산됩니다. 비용 함수는 모델의 성능을 평가하고 최적화 알고리즘(예: 경사 하강법)을 사용하여 모델의 매개변수를 최적화하는 데 사용됩니다.
=> 따라서 단일 훈련 예제에 대한 오류를 계산하는 것이 손실 함수이고, 전체 훈련 세트에 대한 평균 오류를 계산하는 것이 비용 함수입니다.
Gradient Descent

이제 그래디언트 디센트(Gradient Descent) 알고리즘을 사용하여 훈련 세트에서 파라미터 W를 학습하거나 찾는 방법에 대해 이야기해 보겠습니다.

먼저, 로지스틱 회귀 알고리즘과 비용 함수 J를 다시 살펴보겠습니다. 비용 함수 J는 파라미터 W와 B에 따라 정의되며 이 함수는 각 훈련 예제에서 알고리즘의 출력 Y hat I가 실제 레이블 Y I와 어떻게 비교되는지를 측정하는 손실 함수의 평균입니다.

그래디언트 디센트 알고리즘
그래프 상에서 가로 축은 파라미터 W와 B의 공간을 나타내며, 실제로 W는 고차원일 수 있지만 그래프에 나타내기 위해 W를 단일 숫자로 나타내고 B도 마찬가지로 표시합니다. 비용 함수 J(W, B)는 W와 B의 공간상에서 어떤 표면을 형성합니다. 이 표면의 높이는 J(W, B)의 값을 나타내며, 우리의 목표는 이 표면에서 비용 함수 J가 최소가 되는 W와 B의 값을 찾는 것입니다.
이 특정 비용 함수 J는 볼록 함수(convex function)입니다. 즉, 단일 큰 "볼"처럼 생겼습니다. 이것은 비볼록 함수와는 달리 여러 로컬 최적점(local optimum)을 가지지 않습니다. 이 비용 함수 J(W, B)가 볼록 함수로 정의되어 있기 때문에 로지스틱 회귀에서는 이 비용 함수를 사용하는 이유 중 하나입니다.
그래디언트 디센트 알고리즘은 시작점에서 시작하여 가장 가파른 경사 방향으로 한 번에 한 보폭씩 내려가려고 시도합니다. 이렇게 하면 경사하강 방향으로 빠르게 내려가려고 시도합니다. 이것이 그래디언트 디센트의 한 번의 반복(iteration)입니다. 그리고 여러 번의 반복을 통해 전역 최적점(global optimum)에 수렴하거나 전역 최적점에 근접하도록 희망합니다.
Derivatives

마지막으로, 그래디언트 디센트 업데이트 과정을 설명했습니다. 이 과정은 파라미터 W와 B를 반복적으로 업데이트하여 비용 함수 J(W, B)를 최소화하는 방향으로 진행됩니다.

dj(w)/dw 계산:
현재 파라미터 w에서 손실 함수를 w에 대해 편미분한 그래디언트를 계산합니다. 이것은 현재 위치에서 가장 가파른 방향을 나타냅니다. 이 방향으로 이동하면 손실 함수 값이 줄어듭니다.
a(dj(w)/dw) 계산:
학습률 a와 그래디언트 dj(w)/dw를 곱하여 이동 거리를 조절합니다. 학습률은 한 번의 업데이트에서 얼마나 크게 파라미터를 업데이트할지를 제어합니다.
w 업데이트:
계산된 이동 거리를 현재 파라미터 w에서 빼주어 새로운 파라미터 w를 얻습니다. 이렇게 하면 손실 함수를 최소화하는 방향으로 파라미터를 업데이트합니다.
이러한 과정을 반복하여 손실 함수를 최소화하는 최적의 파라미터 w를 찾습니다.
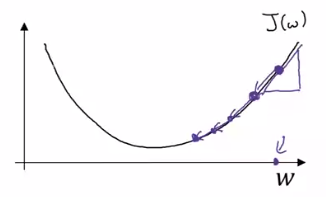
w는 w-a(dw)로 업데이트 된다. 도함수는 양수이다.
비용 함수와 그래디언트 디센트: 비용 함수는 파라미터 w와 b의 함수입니다. 그래디언트 디센트에서는 비용 함수를 최소화하기 위해 반복적으로 w와 b를 업데이트합니다. 업데이트 식은 다음과 같습니다.
w를 업데이트하는 방법: w := w - 학습률 * J(w, b)에 대한 w에 대한 미분
b를 업데이트하는 방법: b := b - 학습률 * J(w, b)에 대한 b에 대한 미분
미분 표기법:
"물결" 기호 (∂)는 편미분을 나타내며 함수의 한 변수에 대한 기울기를 측정합니다.

함수 J가 여러 변수를 가질 경우(입력이 두개), 편미분 기호 (∂)를 사용합니다.
J가 하나의 변수에만 의존하는 함수인 경우 소문자 "d"를 사용합니다.

코드 구현: 코드에서 그래디언트 디센트를 구현할 때, dw는 w를 업데이트할 양을 나타내고, db는 b를 업데이트할 양을 나타냅니다.
*볼록 함수(Convex Function)의 중요한 특징 중 하나는 로컬 최적값(local minimum)이 하나만 존재한다는 것입니다. 다시 말해, 볼록 함수의 모든 로컬 최소값은 동시에 전역 최소값(global minimum)이기도 합니다. 이것은 볼록 함수가 곡면이 항상 위로 볼록하게 휘어지는 형태를 가지기 때문에 발생합니다.
따라서 볼록 함수를 최적화하는 경우, 어떤 초기 조건에서 시작하더라도 경사 하강법(Gradient Descent) 또는 다른 최적화 알고리즘을 사용하여 전역 최소값을 찾을 수 있습니다.

f(a) = 3a 함수를 그래프로 나타냈다. a= 2, f(a)= 6
a=2.001, f(a)= 6.003

녹색으로 강조한 이 작은 삼각형을 살펴보면 a를 오른쪽으로 0.001만큼 밀었을 때 f(a)가 0.003만큼 증가하는 것을 알 수 있습니다.
"미분"이라는 용어는 본질적으로 "기울기"를 의미하며, "미분"이라는 용어를 들을 때 항상 "함수의 기울기"라는 것을 생각하면 됩니다.

더 공식적으로는 기울기는 이 녹색 작은 삼각형의 높이를 밑변으로 나눈 것으로 정의됩니다. 이것은 0.003을 0.001로 나눈 것이며, 기울기가 3이거나 미분이 3이라는 사실은 오른쪽으로 0.001만큼 밀었을 때 f(a)가 밀린 양의 세 배만큼 증가하는 사실을 나타냅니다.
df(a)/da ==d/da(f(a))
"a를 아주 작은 양만큼 밀 때 함수 f(a)의 기울기"
More Derivative Examples

미분 예제 1: f(a) = a²
함수 f(a) = a²를 고려합니다.
이 함수의 미분은 d/da(f(a)) = 2a입니다.
이것은 a값에 따라 기울기가 변한다는 의미입니다.
예를 들어, a=2일 때 기울기는 2x2=4이고, a=5일 때 기울기는 2x5=10입니다.
따라서 a=2에서 함수를 약간 오른쪽으로 밀면 (0.001만큼), 함수 값은 약 0.004만큼 증가합니다.

밑(base)가 자연 상수인 "e"인 로그
미분 예제 2: f(a) = log(a)
함수 f(a) = log(a)를 고려합니다.
이 함수의 미분은 d/da(f(a)) = 1/a입니다.
a값에 따라 기울기가 다르며, a값이 커질수록 기울기는 작아집니다.
예를 들어, a=2에서 기울기는 1/2이므로 a를 0.001만큼 오른쪽으로 밀면 함수 값은 약 0.0005만큼 증가합니다.
미분의 의미: 미분은 함수의 변화율을 나타내며, 함수가 어떤 입력값에서 얼마나 빠르게 변하는지를 나타냅니다.
함수의 도함수는 함수의 기울기.
Computation Graph

이 비디오에서는 뉴럴 네트워크의 계산이 전진 패스 또는 전진 전파 단계로 구성되며, 여기에서 뉴럴 네트워크의 출력을 계산한 다음, 역방향 패스 또는 역전파 단계를 거쳐 그래디언트(기울기) 또는 미분을 계산하는 방법을 설명했습니다. 계산 그래프(Computation Graph)는 왜 이러한 방식으로 구성되는지를 설명합니다.
우리는 이 비디오에서 로지스틱 회귀나 완전한 신경망보다 더 간단한 예제를 사용하여 계산 그래프를 설명할 것입니다. 세 개의 변수 a, b 및 c에 의존하는 함수 J를 계산하려고 한다고 가정해 봅시다. 이 함수는 3(a+bc)로 주어집니다. 이 함수를 계산하는 과정은 실제로 세 단계로 나뉩니다. 첫 번째로, bc를 계산해야 하며, 이것을 변수 u에 저장한다고 가정합시다. 그래서 u=bc입니다. 그런 다음 V=a*u를 계산합니다. 그리고 이것을 V로 나타냅니다. 마지막으로 출력 J는 3V입니다. 이것이 계산하려는 최종 함수 J입니다.
로지스틱 회귀의 경우 J는 최소화하려는 비용 함수입니다. 이 작은 예제에서 보듯이, 왼쪽에서 오른쪽으로 전달하면 J의 값을 계산할 수 있으며, 다음 몇 슬라이드에서는 도함수(기울기)를 계산하기 위해 빨간색 화살표와 같이 오른쪽에서 왼쪽으로 진행하는 역방향 패스가 있음을 볼 것입니다. 이것은 미분을 계산하는 데 가장 자연스러운 방법입니다.
계산 그래프에서 역방향 전파의 한 단계는 최종 출력 변수의 미분을 생성합니다.Derivatives with a Computation Graph

dJ/dv 계산 (0:23부터): dJ/dv는 J를 v로 미세하게 변화시켰을 때 J의 변화량을 나타냅니다. 현재 v=11이고, v를 조금 더 높인다면 (예: 11.001), J도 미세하게 높아집니다 (현재 33에서 33.003으로). 그 결과, v를 0.001만큼 증가시키면 J는 3배만큼 증가합니다. 따라서 dJ/dv = 3입니다.
dJ/da 계산 (2:35부터): dJ/da는 a의 값을 약간 변경하여 J의 값에 어떤 영향을 미치는지를 나타냅니다. a=5일 때, a를 0.001만큼 증가시키면 J는 0.003만큼 증가합니다. 이로 인해 dJ/da = 3입니다.
dJ/du 계산 (3:40부터): dJ/du는 u의 값을 조금 변경하여 J의 값에 어떤 영향을 미치는지를 나타냅니다. u=6일 때, u를 0.001만큼 증가시키면 J는 0.003만큼 증가합니다. 따라서 dJ/du = 3입니다.
각 변수에 대한 도함수를 구하기 위해 연쇄 법칙(Chain Rule)을 사용합니다. 변수를 조금 변경했을 때 J의 변화량은 중간 변수들을 통해 전파됩니다.

"dJdvar"은 역전파 과정에서 최종 출력 변수 J에 대한 미분 값을 나타내는 변수 이름입니다. 이 변수는 주로 코드 작성 시 미분 값을 나타내기 위해 사용됩니다. 따라서 dJdvar은 J에 대한 다른 중간 변수들에 대한 도함수를 계산할 때 사용됩니다. 역전파 과정에서 이러한 미분 값들은 중요하며, 최종 목표는 모델을 최적화하거나 미분 값을 계산하는 데 활용됩니다.

da 는 변수이름임. da는 실제로 dj/da값임
dJ/db 계산 : dJ/db는 b의 값을 약간 변경하여 J의 값을 최소화 또는 최대화하려는 경우에 어떤 영향을 미치는지를 나타냅니다. b를 0.001만큼 증가시키면 J가 0.006만큼 증가합니다. 이로 인해 dJ/db = 6입니다.
dJ/dc 계산 (13:20부터): dJ/dc는 c의 값을 변경하여 J의 값을 나타냅니다. 이 계산은 9입니다.
계산 그래프를 통해, 미분을 계산하는 효율적인 방법은 빨간 화살표 방향으로 계산을 진행하는 것입니다. 먼저 dJ/dv를 계산하고, 이것은 dJ/da와 dJ/du를 계산하는 데 유용하게 사용됩니다. 이것들이 다시 dJ/db 및 dJ/dc를 계산하는 데 도움이 됩니다.
이 비디오의 주요 포인트는 미분 및 계산 그래프를 통해 함수의 도함수를 계산하는 방법을 보여주며, 이것이 로지스틱 회귀와 같은 머신 러닝 모델에서 어떻게 사용되는지를 설명합니다.
Logistic Regression Gradient Descent

이 동영상에서는 로지스틱 회귀(Logistic Regression)의 경사 하강법(Gradient Descent)을 구현하기 위한 중요한 방법과 식을 다루고 있습니다. 주요 내용은 로지스틱 회귀의 경사 하강법을 구현하는 데 필요한 주요 방정식입니다.
로지스틱 회귀의 경사 하강법을 이해하기 위해 계산 그래프(Computation Graph)를 사용하고 있으며, 이것은 로지스틱 회귀의 경사 하강법을 유도하기에 너무 과하게 사용되는 방법이지만, 이러한 아이디어에 익숙해지도록 시작하는 것이 뉴럴 네트워크에 대한 이해를 돕는 데 도움이 될 것입니다.
로지스틱 회귀는 다음과 같이 설정되어 있습니다. 예측인 Y_hat은 Z에 의해 정의되며, Z는 W1, W2 및 B를 포함한 피처 값 X1, X2를 입력으로 사용하여 계산됩니다. 그런 다음 A = Sigma_of_Z로 정의되며, 마지막으로 손실 L은 A,Y로 정의됩니다.
input 벡터인 X1을 구성하는 벡터의 원소들이 x1, x2라고 하면 z값을 구하는 layer의 parameter는 W=[w1 w2]이고 bias b는 하나의 scalar 값인게 맞습니다. 실제로 계산을 보시면 w^Tx를 통해 얻는 것은 벡터의 내적이니 하나의 scalar 값이므로 bias와 더하기 위해서는 b역시 scalar여야합니다.

로지스틱 회귀의 경사 하강법을 구현하려면 손실에 대한 도함수(derivative)를 계산해야 합니다. 이를 위해 먼저 DA(derivative of loss with respect to A)를 계산하며, 그 다음으로 DZ(derivative of loss with respect to Z)를 계산합니다. 이러한 값을 계산하면 W와 B를 얼마나 변경해야 하는지 계산할 수 있습니다.
DA = -Y/A + (1-Y)/(1-A)
DZ = A - Y
DW1 = X1 * DZ
DW2 = X2 * DZ
DB = DZ
한 예제에 대한 경사 하강법 단계를 수행하려면 DZ를 계산하고 DW1, DW2 및 DB를 계산한 다음 위의 공식을 사용하여 가중치 W1, W2 및 편향 B를 업데이트합니다. 이것은 하나의 훈련 예제에 대한 경사 하강법 단계입니다.
하지만 로지스틱 회귀 모델을 훈련시키려면 하나의 훈련 예제가 아니라 M개의 훈련 예제가 있는 훈련 세트에서 학습해야 합니다.
Gradient Descent on m Examples


로지스틱 회귀(Logistic Regression)에서 여러 개의 학습 예제(m training examples)에 대한 경사 하강법(Gradient Descent) 구현 방법에 대한 내용을 설명하고 있습니다. 중요한 이론적인 부분과 수학적인 부분을 중점으로 설명하겠습니다.
비용 함수 J(코스트 함수) 정의:
비용 함수 J는 모델의 예측값($A$)과 실제 레이블($Y$) 사이의 오차를 측정합니다.
로지스틱 회귀의 비용 함수는 로그 손실(log loss 또는 binary cross-entropy)로 정의됩니다.
비용 함수 J는 모든 학습 예제에 대한 손실을 평균한 값으로 정의됩니다.
그래디언트(미분) 계산:
각 학습 예제에 대한 그래디언트(미분 값)를 계산해야 합니다.
for 루프를 사용하여 m개의 학습 예제에 대해 다음 단계를 수행합니다.
z_i = w^T * x_i + b (z_i는 예측값 계산)
a_i = sigmoid(z_i) (a_i는 활성화 함수(시그모이드 함수)를 적용한 예측값)
J += y_i * log(a_i) + (1 - y_i) * log(1 - a_i) (비용 함수 J 업데이트)
dz_i = a_i - y_i (오차 값 계산)
dw_1 += x1_i * dz_i, dw_2 += x2_i * dz_i, ... (가중치 w 업데이트)
db += dz_i (편향 b 업데이트)
이러한 작업을 모든 학습 예제에 대해 반복하고, 마지막에 각 미분 값을 m으로 나누어 평균을 계산합니다.
경사 하강법 업데이트:
각 파라미터(w_1, w_2, b)를 경사 하강법을 사용하여 업데이트합니다.
w_1 = w_1 - learning_rate * dw_1
w_2 = w_2 - learning_rate * dw_2
b = b - learning_rate * db
반복:
위 단계를 여러 번 반복하여 모델을 학습합니다.
이론적으로, 이 방법은 학습 데이터셋에 대해 경사 하강법을 구현하는 방법을 설명하고 있습니다. 그러나 이러한 구현 방식은 두 가지 약점이 있는데, 첫째로 학습 예제(m)에 대한 for 루프와 두 번째로 특성(feature)에 대한 for 루프가 필요하다는 것입니다. 이는 딥 러닝 알고리즘을 구현할 때 효율성이 떨어지게 만들 수 있습니다.
딥 러닝에서는 명시적인 for 루프를 사용하지 않고 벡터화(Vectorization) 기법을 활용하여 계산을 최적화합니다. 이러한 벡터화 기법을 사용하면 코드의 실행 속도를 향상시키고 대용량 데이터셋에 대응할 수 있습니다. 이것이 딥 러닝 분야에서 중요한 개념 중 하나입니다. 앞으로의 비디오에서는 벡터화에 대해 자세히 다루게 됩니다.
--https://community.deeplearning.ai/t/derivation-of-dl-dz/165
DeepLearning.AI
Powered by Discourse, best viewed with JavaScript enabled
community.deeplearning.ai
Vectorization

비 벡터화 구현 or 벡터화 구현 비교
import time
a= np.random.rand(1000000)
b=np.random.rand(1000000)
tic = time.time()
c=np.dot(a,b)
toc=time.time()
print("vectorized version:",str(1000*(toc-tic)))
c=0
tic=time.time()
for i in range(1000000):
c+=a[i]*b[i]
toc=time.time()
print("for loop:",str(1000*(toc-tic)))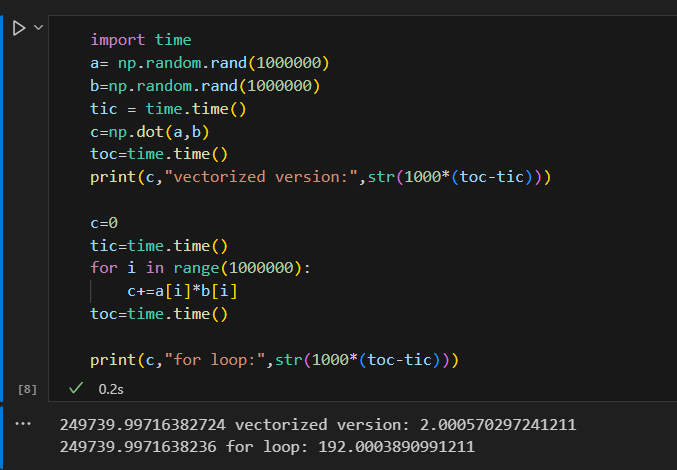
for 루프를 쓰면 더 오래걸림을 확인.
실제로 약 200배 이상 느림.
More Vectorization Examples

for 루프를 피해야함.
벡터화란, 명시적인 for 루프를 피하고 내장 함수나 다른 방법을 사용하여 코드를 최적화하는 기술입니다.
딥러닝 또는 회귀 모델을 프로그래밍할 때 명시적인 for 루프를 피하려고 노력해야 합니다.
벡터화를 사용하면 코드 실행 속도가 향상되며, 특히 큰 데이터셋을 처리할 때 유용합니다.
예제:

벡터화의 예제로 행렬과 벡터 연산, 지수 연산에 대한 내용을 다루고 있습니다.
행렬과 벡터 연산을 비벡터화된 버전과 벡터화된 버전으로 비교하고 있으며, 벡터화된 버전이 더 빠른 속도로 실행됨을 보여줍니다.
내장 함수를 활용하면 명시적인 for 루프를 피할 수 있으며, 이렇게 하면 코드가 간결해지고 실행 속도가 향상됩니다.
NumPy 라이브러리:
NumPy는 벡터화된 연산을 지원하는 파이썬 라이브러리로, 다양한 벡터 연산 함수를 제공합니다.
np.exp(v), np.log(v), np.abs(v), np.maximum(v, 0), v**2, 1/v 등의 함수를 활용하여 벡터 연산을 간단하게 수행할 수 있습니다.
np.exp(v): 지수 함수 (Exponential Function)
입력 벡터 v의 각 원소에 대해 지수 연산을 수행하여 반환합니다.
예를 들어, np.exp([1, 2, 3])는 [e, e^2, e^3]을 반환합니다. 여기서 e는 자연 로그의 밑수인 오일러 수(약 2.71828)를 나타냅니다.
np.log(v): 로그 함수 (Natural Logarithm)
입력 벡터 v의 각 원소에 대해 자연 로그 연산을 수행하여 반환합니다.
예를 들어, np.log([1, e, e^2])는 [0, 1, 2]를 반환합니다.
np.abs(v): 절댓값 함수 (Absolute Value)
입력 벡터 v의 각 원소에 대해 절댓값을 계산하여 반환합니다.
예를 들어, np.abs([-2, 3, -4])는 [2, 3, 4]를 반환합니다.
np.maximum(v, 0): 원소별 최댓값 함수
입력 벡터 v의 각 원소와 0 중에서 큰 값을 선택하여 반환합니다.
이 함수를 사용하면 입력 벡터의 각 원소를 0 이상으로 만들 수 있습니다. 음수 값은 0으로 변환됩니다.
예를 들어, np.maximum([-2, 3, -4], 0)은 [0, 3, 0]을 반환합니다.
v**2: 제곱 연산
입력 벡터 v의 각 원소를 제곱한 값을 반환합니다.
예를 들어, np.array([1, 2, 3])**2는 [1, 4, 9]를 반환합니다.
1/v: 역수 연산
입력 벡터 v의 각 원소에 대해 역수(1을 나누기)를 계산하여 반환합니다.
주의: v의 원소 중에 0이 있는 경우, 해당 원소는 역수를 계산할 수 없으므로 경고나 오류가 발생할 수 있습니다.
이러한 내장 함수를 활용하면 for 루프를 사용하지 않고도 벡터 연산을 수행할 수 있습니다.

2번째 for 루프 제거

방법
x표시한 부분 대신 오른쪽 초록색 수식 넣기
벡터화된 코드 설명:
Z = np.dot(w.T, X) + b: 모든 학습 예제에 대한 예측 Z 값을 한 번에 계산합니다. 이렇게 하면 두 번째 for 루프가 없어졌습니다.
A = sigmoid(Z): Z 값을 시그모이드 함수에 적용하여 활성화 값을 계산합니다.
dz = A - Y: 예측된 활성화 값과 실제 레이블 간의 차이를 계산합니다.
dw = np.dot(X, dz.T) / m: 벡터화된 연산을 사용하여 모든 학습 예제에 대한 dw를 한 번에 계산합니다.
Vectorizing Logistic Regression

이 비디오에서는 로지스틱 회귀의 구현을 벡터화하는 방법에 대해 설명하고, 명시적인 for 루프 없이 전체 학습 데이터 세트에 대한 하나의 경사 하강 단계를 구현하는 방법을 살펴보겠습니다. 중요한 수학적인 부분과 개념을 설명해드리겠습니다.
벡터화(Vectorization) 개념: 벡터화는 NumPy와 같은 라이브러리를 사용하여 반복문 없이 행렬 및 벡터 연산을 수행하는 기법입니다. 이를 통해 코드를 효율적으로 만들 수 있으며 연산 속도를 높일 수 있습니다.
행렬 및 벡터 정의:
훈련 입력 데이터를 포함하는 행렬 X는 각 열이 서로 다른 훈련 예제로 구성되며, X는 NX x M 행렬입니다. 여기서 NX는 특성(feature) 수이고, M은 훈련 예제 수입니다.
행렬 X는 각 열이 서로 다른 훈련 예제에 해당하는 입력 데이터입니다.

Z 값 벡터화:
Z1, Z2, ..., ZM의 예측을 모두 한 번에 계산하려면, 행렬 X와 가중치 벡터 W를 사용하여 Z 값을 계산할 수 있습니다.
Z = np.dot(W.T, X) + B로 표현할 수 있으며, 이렇게 하면 각 훈련 예제에 대한 Z 값이 한 번에 계산됩니다. 이 코드는 벡터화되어 있어서 명시적인 for 루프를 사용하지 않고도 모든 Z 값을 계산할 수 있습니다.
활성화 값 A의 벡터화:
활성화 값 A1, A2, ..., AM을 모두 한 번에 계산하기 위해 소문자 A를 벡터화할 수 있습니다.
벡터화된 시그모이드 함수를 사용하여 capital A를 계산하면 각 훈련 예제에 대한 활성화 값이 동시에 계산됩니다.
백워드 패스와 그래디언트 계산:
벡터화를 사용하여 backpropagation 단계에서 그래디언트(기울기)를 효율적으로 계산할 수 있습니다.
Vectorizing Logistic Regression's Gradient Output

이 비디오에서는 벡터화(Vectorization)를 사용하여 로지스틱 회귀의 그래디언트(gradient) 계산을 수행하는 방법과 전체 학습 데이터 세트에 대한 효율적인 로지스틱 회귀 구현을 설명하고 있습니다.
a (소문자 a): a는 활성화(activation)를 나타내는 변수로, 로지스틱 회귀에서는 시그모이드 함수를 통해 계산된 예측값(출력)을 의미합니다. 즉, a는 각 학습 샘플에 대한 모델의 예측값 벡터입니다. a는 다음과 같이 표현됩니다.
a = [a1, a2, ..., aM]
여기서 M은 학습 샘플의 수이며, ai는 각 학습 샘플에 대한 예측값입니다.
y (소문자 y): y는 실제 레이블(타겟) 값을 나타내는 변수로, 로지스틱 회귀에서는 각 학습 샘플의 실제 클래스(레이블)를 나타냅니다. y는 다음과 같이 표현됩니다.
y = [y1, y2, ..., yM]
여기서 yi는 각 학습 샘플에 대한 실제 클래스(레이블)입니다.
따라서 a는 예측값의 벡터이고, y는 실제 클래스(레이블)의 벡터
=---벡터화(Vectorization) 개요:
벡터화는 NumPy와 같은 라이브러리를 사용하여 반복문 없이 행렬 및 벡터 연산을 수행하는 기법입니다.
이를 통해 코드를 효율적으로 만들 수 있으며 연산 속도를 높일 수 있습니다.
그래디언트 계산의 벡터화:
이전 비디오에서는 벡터화를 사용하여 예측 값을 계산했습니다.
이번 비디오에서는 그래디언트 계산에도 벡터화를 적용하여 M개의 학습 샘플에 대한 그래디언트 계산을 동시에 수행하는 방법을 설명합니다.
그래디언트 계산의 벡터화 방법:
이전 슬라이드에서 dz 값을 계산하는 방법을 보았습니다. 이를 다시 살펴보면 dz1, dz2, ..., dzM을 모두 계산하려면 lowercase z 변수들을 가로로 쌓은 벡터 dZ를 정의할 수 있습니다.
dZ = [dz1, dz2, ..., dzM] 또는 m 차원의 행 벡터로 정의됩니다.
이 때, dZ = A - Y로 계산됩니다. 여기서 A는 활성화 값 벡터 [a1, a2, ..., aM], Y는 실제 값 벡터 [y1, y2, ..., yM]로 정의됩니다.

벡터화된 db 계산:
db를 벡터화하기 위해서는 모든 dz 값을 더한 후 M으로 나누어 주면 됩니다.
db = (1/M) * np.sum(dZ)로 계산됩니다.
벡터화된 dw 계산:
dw를 벡터화하려면 행렬 X와 dz transpose를 곱한 후 M으로 나누어 주면 됩니다.
dw = (1/M) * X * dZ.transpose()로 계산됩니다.
전체 구현:
이러한 벡터화된 계산을 사용하여 전체 로지스틱 회귀 구현을 단순하게 표현할 수 있습니다.
forward propagation 및 back propagation을 명시적인 for 루프 없이 수행할 수 있으며, 모든 학습 샘플에 대한 예측 및 그래디언트 계산을 동시에 수행합니다.
반복(iteration)의 중요성:
하나의 반복(iteration)은 for 루프 없이 수행할 수 있지만, 여러 번의 반복(iterations)을 수행하려면 반복(iteration) 수에 대한 for 루프가 필요합니다.
여러 번의 경사 하강(iterations)을 수행하려면 반복(iteration) 수에 대한 for 루프를 추가해야 합니다.
Broadcasting in Python


이 동영상에서는 Python의 브로드캐스팅(Broadcasting)에 대한 내용을 다루고 있습니다. 브로드캐스팅은 Python 코드를 더 빠르게 실행할 수 있는 기술 중 하나로, 배열 연산을 간단하게 처리할 수 있도록 도와줍니다.
axis 설명

# Matrix A with calorie information
A = np.array([[56, 0.0, 4.4,68.0],
[1.2, 104.0, 52.0, 8.0],
[1.8, 135.0, 99.0, 0.9]])
# Sum of columns (total calories for each food)
#수직으로 합산
cal = A.sum(axis=0)
print(A,cal,cal.reshape(1, 4) )
# Calculate percentages
percentage = A / cal.reshape(1, 4) * 100
print(percentage)
브로드캐스팅의 개념: 브로드캐스팅은 서로 다른 모양(shape)을 가진 배열 간의 연산을 가능하게 하는 기술입니다. 예를 들어, (m, n) 모양의 배열과 (1, n) 모양의 배열 간의 연산을 할 때, Python은 자동으로 (m, n) 모양으로 브로드캐스팅하여 요소별 연산을 수행합니다.
브로드캐스팅 예제: 동영상에서는 칼로리 정보가 포함된 100그램의 음식 데이터를 사용한 예제를 통해 브로드캐스팅을 설명합니다. 각 음식의 탄수화물, 단백질, 지방 칼로리의 비율을 계산하는 작업을 브로드캐스팅을 사용하여 수행합니다. 이를 통해 Python에서 요소 간 연산을 보다 간단하게 수행할 수 있음을 보여줍니다.

브로드캐스팅 종류: 동영상에서는 다양한 브로드캐스팅 종류를 설명합니다. 예를 들어, (m,n) 배열과 (1,n) 배열 간의 연산, (m,n) 배열과 (m,1) 배열 간의 연산, 그리고 (m,1) 배열과 스칼라 값 간의 연산 등이 다루어집니다.
A Note on Python/Numpy Vectors
import numpy as np
a = np.random.randn(5)
print(a,a.shape,'\n전치',a.T,'\nnp.dot(a,a.T)',np.dot(a,a.T))
전치값 등 계산에 버그 발생함.
1순위 배연인 데이터 구조를 사용하지 않아야함.
#열벡터로 생성
a= np.random.randn(5,1)
print(a)
print(a.T)
print(np.dot(a,a.T))
위의 a.shape=(5,)와 같은 것을 rank 1 array라함.
Rank 1 배열: -->사용 x
Rank 1 배열은 Python에서 특별한 형태의 배열로, 행 벡터나 열 벡터로 일관되게 동작하지 않아 혼란스러운 결과를 초래할 수 있습니다.
Rank 1 배열 대신 (n,1) 또는 (1,n) 배열을 사용하여 열 벡터 또는 행 벡터로 명시적으로 정의하는 것이 좋습니다.
Assertion 문:
Assertion 문을 사용하여 벡터나 행렬의 차원을 확인하는 것이 유용하며, 코드를 문서화하는 데 도움이 됩니다.
Assertion은 코드 검증에 도움이 되며, 차원 확인에 사용할 수 있습니다.

Rank 1 배열을 다른 형태로 변환:
Rank 1 배열을 다른 형태로 변환하여 일관된 동작을 보장할 수 있습니다.
Explanation of Logistic Regression Cost Function (Optional)

이 비디오에서는 로지스틱 회귀의 비용 함수에 대한 이론적인 근거와 의미를 설명합니다.
로지스틱 회귀에서, 예측값 y hat은 sigmoid 함수를 통과한 결과로 나타낼 수 있습니다. 이때 sigmoid 함수는 다음과 같이 정의됩니다:
sigmoid(z) = 1 / (1 + e^(-z))
우리는 y hat을 p(y=1|x)로 해석하고자 합니다. 즉, y hat은 입력 특성 x에 대한 y=1의 확률로 해석됩니다. 따라서 y=1이라면 y given x의 확률은 y hat이며, y=0이라면 y given x의 확률은 1 - y hat입니다.
두 가지 경우에 대한 확률을 종합하여 p(y|x)를 정의하고자 합니다. 이를 위해 다음과 같은 방정식을 사용합니다:
p(y|x) = y hat^y * (1 - y hat)^(1 - y)
이 방정식은 y가 1 또는 0인 두 가지 경우에 대한 확률을 정확하게 나타냅니다. 이것은 로지스틱 회귀 모델에서 p(y|x)를 정의하는 올바른 방법입니다.
또한 로그 함수가 단조 증가 함수이기 때문에, 로그우도를 최대화하는 것은 우도를 최대화하는 것과 동일한 결과를 가져옵니다. 따라서 로그우도를 계산하면 다음과 같습니다:
log(p(y|x)) = y * log(y hat) + (1 - y) * log(1 - y hat)
마지막으로, 전체 교육 세트에 대한 비용 함수를 구하기 위해 로그우도를 모두 더하고 음수 부호와 1/m 스케일링 요소를 추가합니다. 이로써 비용 함수 J(w,b)가 정의됩니다.
J(w,b) = (-1/m) * Σ [y * log(y hat) + (1 - y) * log(1 - y hat)]
따라서 로지스틱 회귀의 비용 함수 J(w,b)를 최소화함으로써, 우리는 실제로 로지스틱 회귀 모델에 대한 최대 우도 추정을 수행하고 있습니다. 이는 교육 예제가 독립 동일하게 분포되었다는 가정 하에 이루어집니다.
| 로그우도(Log Likelihood)는 최대우도추정(Maximum Likelihood Estimation, MLE)에서 사용되는 개념으로, 어떤 확률분포에서 관측된 데이터가 가장 가능성 높게 발생한 것으로 추정하는 방법 중 하나입니다. 로그우도는 확률분포의 파라미터를 조정하여 주어진 데이터의 확률을 최대화하는 파라미터 값을 찾는 과정에서 유용하게 사용됩니다. 로지스틱 회귀의 경우, 이진 분류 문제에서 사용되며, 관측된 데이터와 모델의 예측 사이의 차이를 최소화하기 위해 로그우도를 최대화하는 파라미터를 찾습니다. 로그우도는 다음과 같이 정의됩니다. 로그우도(L) = Σ [y * log(y hat) + (1 - y) * log(1 - y hat)] 여기서: L: 로그우도 Σ: 모든 훈련 예제에 대한 합계 y: 실제 관측된 레이블 (0 또는 1) y hat: 모델의 예측값 (0과 1 사이의 확률) |
