Deep Learning Specialization - Neural Networks and Deep Learning [3]
학습 목표
- Describe hidden units and hidden layers
- Use units with a non-linear activation function, such as tanh
- Implement forward and backward propagation
- Apply random initialization to your neural network
- Increase fluency in Deep Learning notations and Neural Network Representations
- Implement a 2-class classification neural network with a single hidden layer
- Compute the cross entropy loss
한국어로 번역:
"하나의 은닉 레이어를 사용하여 순방향 전파 및 역전파를 이용하여 신경망 구축하기"
학습 목표:
은닉 유닛과 은닉 레이어를 설명합니다.
tanh와 같은 비선형 활성화 함수를 사용하는 유닛을 사용합니다.
순방향 전파와 역전파를 구현합니다.
신경망에 무작위 초기화를 적용합니다.
딥 러닝 표기법과 신경망 표현을 능숙하게 이해합니다.
하나의 은닉 레이어를 사용하여 2 클래스 분류 신경망을 구현합니다.
크로스 엔트로피 손실을 계산합니다.
Neural Networks Overview

이번 주에는 신경망을 구현하는 방법을 배웠습니다.
신경망은 여러 개의 유닛을 쌓아 올린 구조로, 각 유닛은 로지스틱 회귀와 유사한 계산을 수행합니다.
각 레이어를 가리키는 표기법은 [1]은 첫 번째 레이어를, [2]는 두 번째 레이어를 의미합니다.
각 레이어에서는 먼저 z를 계산하고, 그 다음에 a를 계산합니다 (a는 로지스틱 회귀의 ŷ와 동일합니다).
신경망은 역전파(backpropagation)를 사용하여 da, dz, dw, db 등의 도함수를 계산합니다.
역전파 과정은 신경망 그래프에서 빨간색 화살표로 나타납니다.
로지스틱 회귀는 신경망의 기본 구성 요소이며, 각 레이어에서 반복적으로 사용됩니다.
이러한 개념에 대한 자세한 내용은 다음 비디오에서 자세히 다룰 예정입니다.
요약하면, 신경망은 로지스틱 회귀를 여러 레이어로 쌓아 올린 구조로, 각 레이어에서 z와 a를 계산하고, 역전파를 사용하여 도함수를 계산하고 네트워크의 매개변수를 조정합니다.
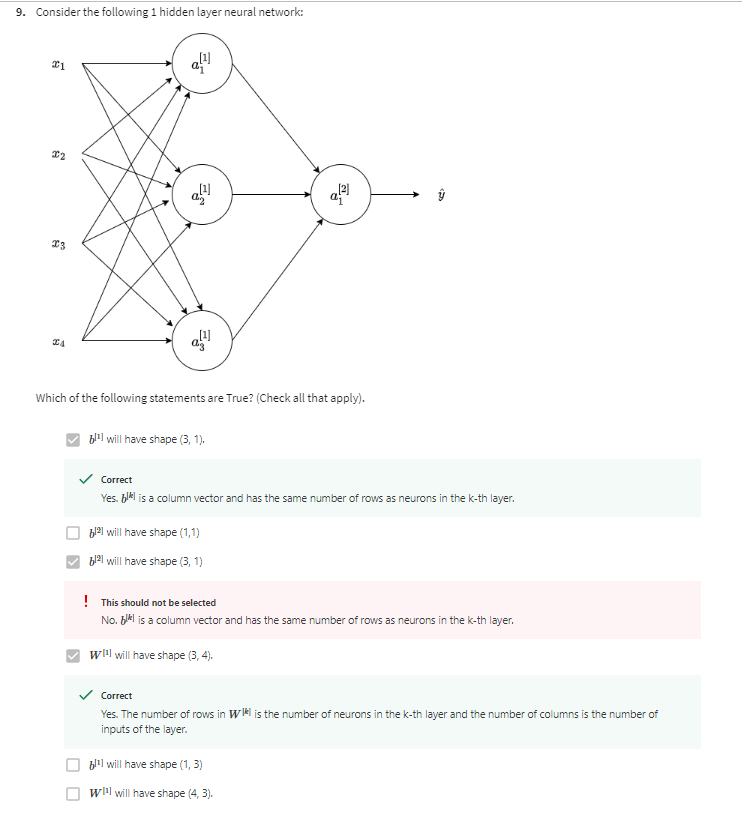
Neural Network Representation

입력층은 안센다.
신경망의 구성:
신경망은 입력 층(input layer), 은닉 층(hidden layer), 출력 층(output layer)으로 구성됩니다.
입력 층에는 입력 특성(x1, x2, x3)이 수직으로 쌓여 있습니다.
은닉 층은 중간에 위치한 층으로 "은닉(hidden)"이라는 용어는 훈련 세트에서 이 층의 값이 관측되지 않음을 나타냅니다.
출력 층은 하나의 노드로 구성되며 예측 값을 출력합니다(ŷ).
표기법:
입력 특성을 나타내는 벡터 "X" 대신 "a[0]"를 사용합니다.
"a"라는 용어는 활성화(activations)를 나타내며, 각 층이 다음 층으로 전달하는 값입니다.
은닉 층에서는 "a[1]"과 같은 활성화 값이 생성되며, 각 노드는 "a1[1]", "a2[1]" 등의 값을 생성합니다.
출력 층에서는 "a[2]"가 생성되며, 이 값은 "ŷ"로 사용됩니다.
층의 개수:
신경망에서는 입력 층을 제외한 층의 개수를 카운트합니다.
따라서 이 예제에서는 입력 층(층 0), 은닉 층(층 1), 출력 층(층 2)으로 총 3개의 층이 있지만, 일반적으로 이를 2개의 층 신경망으로 부릅니다.
매개변수:
은닉 층과 출력 층은 각각 매개변수 w와 b와 관련이 있습니다.
이러한 매개변수는 층에 대해 명시적으로 표기되며, 예를 들어 은닉 층의 매개변수는 "w[1]"과 "b[1]"로 표시됩니다.
매개변수의 차원은 향후에 자세히 다루게 되며 중요한 역할을 합니다.
Computing a Neural Network's Output

신경망의 연산 단계:
신경망은 여러 단계의 연산을 수행하여 출력을 계산합니다.
각 노드는 두 단계의 연산을 수행합니다. 먼저 "z"를 계산하고, 다음으로 "a"를 계산합니다.
"z"는 가중치(w), 입력(x), 편향(b)을 사용하여 계산됩니다.
"a"는 "z"에 시그모이드 함수를 적용하여 계산됩니다.
표기법:
"a[l]"에서 "l"은 층(layer)을 나타내며, "i"는 해당 층의 노드(node)를 나타냅니다.
예를 들어, "a1[1]"은 첫 번째 은닉 층의 첫 번째 노드에서의 활성화를 나타냅니다.
이러한 표기법을 사용하여 각 노드의 연산과 결과를 구분합니다.
은닉 층의 계산:
은닉 층의 각 노드는 "z"를 계산하고 시그모이드 함수를 사용하여 "a"를 계산합니다.
각 노드에서 수행되는 계산은 입력과 가중치에 따라 다르며, 각 노드의 출력은 "a[l]"로 표시됩니다.
여러 은닉 층과 노드가 있을 경우, 각각의 계산이 반복됩니다.

[1]
신경망 노드의 연산:
각 노드는 "z"와 "a" 두 단계의 연산을 수행합니다.
"z"는 입력(x), 가중치(w), 편향(b)를 사용하여 계산됩니다.
"a"는 "z"에 시그모이드 함수를 적용하여 계산됩니다.
이러한 계산은 각 노드에서 수행되며, 노드에 대한 표기법은 "[l]"과 "[i]"를 사용하여 층과 노드를 나타냅니다.
은닉 층의 연산:
은닉 층의 각 노드는 "z"와 "a" 값을 계산합니다.
이 값들은 각 노드마다 다르며, "z[1]"와 "a[1]" 등으로 표기됩니다.
은닉 층의 연산은 입력과 가중치를 행렬 연산으로 처리합니다.
행렬 및 벡터 표기법:
여러 노드와 층에서 수행되는 연산은 행렬과 벡터 표기법을 사용하여 효율적으로 처리됩니다.
"W[1]"는 가중치 행렬을 나타내며, "b[1]"은 편향 벡터를 나타냅니다.
입력과 가중치를 곱하고 편향을 더하여 "z[1]"을 계산합니다.
"a[1]"은 "z[1]"에 시그모이드 함수를 적용한 결과를 나타냅니다.
[2]신경망의 연산:
각 노드는 "z"와 "a"를 계산합니다.
"z"는 입력과 가중치를 사용하여 계산되며, "a"는 "z"에 시그모이드 함수를 적용하여 계산됩니다.
노드는 층과 노드 번호로 표기됩니다.
은닉 층 연산:
은닉 층의 노드는 "z"와 "a" 값을 계산합니다.
각 노드는 다른 값이며 "[l]"과 "[i]"로 표기됩니다.
연산은 행렬과 벡터 표기법을 사용하여 효율적으로 처리됩니다.
행렬과 벡터 표기법:
가중치 행렬은 "W[l]"로 표기되고, 편향 벡터는 "b[l]"로 표기됩니다.
행렬 및 벡터 연산을 통해 "z"와 "a"를 계산합니다.
여러 노드의 결과를 열 벡터로 스택하여 "z"와 "a"를 표현합니다.
출력 계산:
신경망의 출력은 "a[2]" 또는 "ŷ"로 표기되며 시그모이드 함수를 적용한 "z[2]"로부터 계산됩니다.

Vectorizing Across Multiple Examples

이 동영상에서는 여러 학습 샘플을 벡터화하는 방법에 대해 배울 것입니다. 결과는 로지스틱 회귀와 매우 유사하게 나타납니다. 여러 학습 샘플을 행렬의 다른 열로 결합하면 이전 비디오의 방정식을 사용하여 신경망이 동시에 모든 학습 샘플의 결과를 계산할 수 있게 됩니다. 그러므로 이것이 어떻게 동작하는지 자세히 살펴보겠습니다.
개요:
이전 비디오에서 얻은 4개의 방정식은 z1, a1, z2 및 a2를 계산하는 방법을 보여줍니다.
하나의 학습 샘플에 대한 입력 특징 벡터 x가 주어지면 a2 = ŷ를 생성할 수 있습니다.
다중 학습 샘플:
m개의 학습 샘플이 있다고 가정하면 각 학습 샘플에 대해 동일한 과정을 반복해야 합니다.
x(1)은 첫 번째 학습 샘플에 대한 예측 ŷ(1)을 생성합니다.
마찬가지로 x(2)는 두 번째 학습 샘플에 대한 ŷ(2)를 생성하고, x(m)은 m번째 학습 샘플에 대한 ŷ(m)을 생성합니다.
벡터화:
벡터화를 사용하면 모든 학습 샘플에 대한 예측을 동시에 계산할 수 있습니다.
새로운 인덱스 [i]를 추가하여 표기합니다. 이는 학습 샘플 [i]를 나타냅니다.
a2와 같이 i에 대한 슈퍼스크립트 [i]를 추가하여 표시합니다.
이렇게 하면 각 학습 샘플에 대한 결과를 계산할 수 있습니다.
수식 벡터화:
수식을 벡터화하면 모든 학습 샘플에 대한 결과를 빠르게 계산할 수 있습니다.
반복문 없이 한 번에 모든 예측을 얻을 수 있습니다.
예를 들어 z1 = W[1] * x(i) + b[1], a1 = sigmoid(z1)와 같이 i에 대한 인덱스를 추가하여 모든 변수를 벡터화합니다.

행렬 구성:
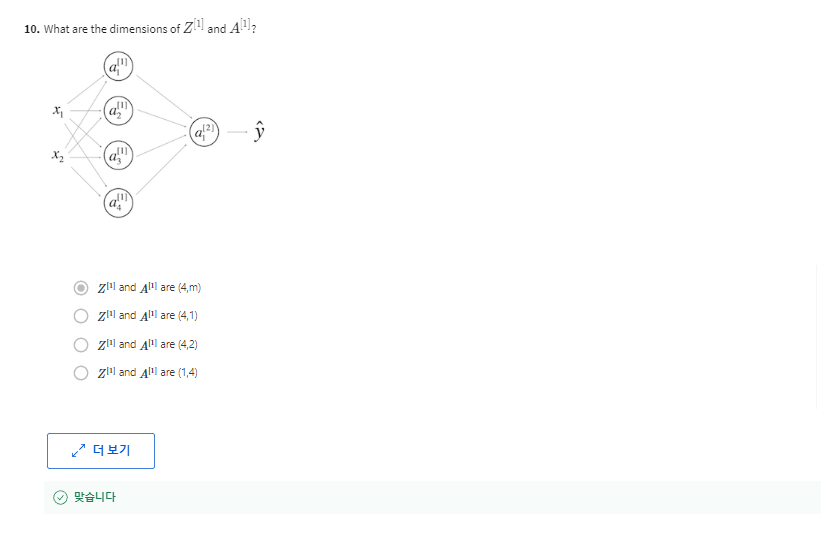
학습 샘플을 나타내는 행렬 X를 정의합니다. X는 학습 샘플들을 서로 다른 열에 쌓은 형태입니다. 따라서 X의 차원은 (n x m)이 됩니다.
벡터화된 구현:
다음으로, 벡터화된 버전으로 구현해야 할 내용을 알아봅니다.
Z[1] = W[1]X + b[1], A[1] = sigmoid(Z[1])을 계산하여 첫 번째 레이어의 활성화 값을 얻습니다.
Z[2] = W[2]A[1] + b[2], A[2] = sigmoid(Z[2])를 계산하여 두 번째 레이어의 활성화 값을 얻습니다.
인덱싱:
이러한 행렬을 인덱싱할 때, 가로 방향은 다른 학습 샘플을 나타내며, 세로 방향은 다른 은닉 노드를 나타냅니다.
가로 방향으로 이동하면 다른 학습 샘플을 탐색하고, 세로 방향으로 이동하면 다른 은닉 유닛을 탐색합니다.
Explanation for Vectorized Implementation

벡터화 구현의 정당성:
여러 학습 샘플을 효율적으로 처리하기 위한 벡터화된 구현이 왜 옳은지에 대한 추가적인 근거를 제시합니다.
일단 b를 무시하고 b=0이라고 가정하여 설명을 단순화합니다.
w1은 행렬이므로 다양한 행이 있습니다.
x1에 대한 계산에서 w1 * x1은 열 벡터를 생성하고 이 벡터는 z12입니다.
x2에 대한 계산에서 w1 * x2는 다른 열 벡터를 생성하고 이 벡터는 z13입니다.
훈련 세트 행렬 X는 x1, x2, x3 등의 벡터를 수직으로 쌓아 만듭니다.
이 행렬 X를 w로 곱하면 Z1 행렬이 생성됩니다. Z1은 z11, z12, z13 등의 열 벡터로 구성됩니다.
이것은 각 학습 샘플에 대한 z 값을 열로 쌓은 것입니다.
마무리:
z1 = w1x + b1이 벡터화된 구현의 첫 번째 단계임을 정당화했습니다.

x는 a0과 동일합니다:
x와 입력 특성 벡터 a0이 동일하다는 사실을 상기시켜줍니다.
따라서 xi는 a0i와 동일하다.
유사한 구조:
첫 번째 방정식을 z1 = w1a0 + b1로 다시 작성할 수 있으며, a0을 사용한 것을 볼 수 있습니다.
두 개의 방정식 쌍이 매우 유사하며, 인덱스만 한 단계씩 증가합니다.
이것은 다른 뉴럴 네트워크 층이 거의 동일한 계산을 반복하거나 비슷한 작업을 수행함을 보여줍니다.
깊은 뉴럴 네트워크:
두 층 뉴럴 네트워크 예제를 제시하고, 다음 주에는 더 깊은 네트워크를 다룬다는 언급이 있습니다.
깊은 뉴럴 네트워크도 기본적으로 이 두 단계를 반복하여 작동한다는 사실을 보여줍니다.
Activation Functions

시그모이드 함수 (Sigmoid Function):
수식: a = 1 / (1 + e^(-z))
출력 범위: 0에서 1 사이
주로 이진 분류 문제의 출력층에서 사용됩니다.
그러나 시그모이드 함수는 큰 입력값에 대해 기울기가 매우 작아져서 그래디언트 소실 문제를 야기할 수 있습니다.
하이퍼볼릭 탄젠트 함수 (Hyperbolic Tangent Function, tanh):
수식: a = (e^z - e^(-z)) / (e^z + e^(-z))
출력 범위: -1에서 1 사이
시그모이드와 유사하지만 출력 범위가 -1부터 1까지로 중심이 0이며, 그래서 활성화 출력의 평균이 0 주변에 있습니다. 이로 인해 그래디언트 소실 문제가 일어나지 않습니다.
ReLU 함수 (Rectified Linear Unit):
수식: a = max(0, z)
출력 범위: 0보다 큰 값은 입력을 그대로 반환하고, 0 이하의 값은 0으로 출력합니다.
현재 가장 많이 사용되는 활성화 함수 중 하나입니다. 빠른 수렴과 학습을 통해 다양한 네트워크 구조에서 잘 작동합니다.
하지만 입력이 음수인 경우에는 그래디언트가 0이 되어 dead ReLU 문제가 발생할 수 있습니다.
Leaky ReLU 함수 (Leaky Rectified Linear Unit):
수식: a = max(αz, z) (α는 작은 양수)
출력 범위: 입력이 양수인 경우는 그대로 반환하고, 음수인 경우 작은 기울기 α를 곱해줍니다.
dead ReLU 문제를 완화하기 위해 제안되었으며, 하이퍼파라미터 α는 일반적으로 0.01과 같은 작은 값으로 설정됩니다.
활성화 함수 선택은 네트워크의 성능에 큰 영향을 미치므로 주어진 문제와 데이터에 따라 적절한 함수를 선택하는 것이 중요합니다. 실험을 통해 최적의 활성화 함수를 찾아내고, 학습 속도와 안정성을 고려하여 조정하는 것이 일반적인 접근 방식입니다. 이러한 함수들은 네트워크가 복잡한 비선형 관계를 모델링하고 효율적으로 학습할 수 있도록 도와줍니다.
Why do you need Non-Linear Activation Functions?

네트워크에서 비선형 활성화 함수를 사용하는 이유는 네트워크가 복잡한 데이터 패턴을 학습하고 표현하기 위해 필요합니다. 활성화 함수가 없다면, 네트워크는 선형 함수의 조합만 계산할 수 있으며, 이는 복잡한 함수를 모델링하는 데 제한적입니다.
여기서 주목할 점은 활성화 함수를 사용하지 않는다면 네트워크는 각 층에서 입력의 선형 변환만 수행할 것이며, 이는 여러 층을 쌓더라도 하나의 선형 함수로 축소됩니다. 따라서 신경망의 층을 추가하는 의미가 없어집니다.
특정한 경우를 예로 들면, 활성화 함수를 사용하지 않거나 선형 활성화 함수 (항등 함수)를 사용하는 것은 네트워크를 깊게 만들어도 효과가 없습니다. 즉, 여러 층의 합성 함수가 결국 선형 함수가 되어 더 복잡한 표현을 학습하지 못합니다.
활성화 함수가 필요한 예로 회귀 문제를 들 수 있습니다. 회귀 문제에서 출력이 실수값인 경우, 선형 활성화 함수를 사용하여 출력이 실수 범위에서 계산될 수 있습니다. 그러나 이외의 다른 경우에는 비선형 활성화 함수를 사용하여 네트워크가 비선형 함수를 학습할 수 있도록 해야 합니다.
결론적으로, 활성화 함수의 주요 역할은 네트워크가 비선형성을 표현하고 복잡한 데이터 패턴을 학습할 수 있도록 하는 것입니다. 이를 통해 신경망은 다양한 종류의 문제를 해결할 수 있으며, 최적의 활성화 함수를 선택하는 것이 중요합니다.
Derivatives of Activation Functions

신경망의 역전파를 구현할 때 활성화 함수의 미분(도함수)을 계산해야 합니다. 활성화 함수의 미분을 어떻게 계산할 수 있는지 알아보겠습니다.
시그모이드 활성화 함수 (Sigmoid Activation): 시그모이드 함수의 미분은 다음과 같이 계산됩니다.
g(z)가 시그모이드 함수인 경우, g'(z)는 g(z)(1 - g(z))로 정의됩니다.
이 식은 g(z)와 (1 - g(z))를 곱한 값입니다. 이를 통해 z가 매우 크면 미분 값은 0에 가깝고, z가 매우 작으면 미분 값은 또 다시 0에 가까워지며, z가 0에 가까울 때 미분 값은 1/4에 가까워집니다.
하이퍼볼릭 탄젠트 활성화 함수 (Tanh Activation): 하이퍼볼릭 탄젠트 함수의 미분은 다음과 같이 계산됩니다.
g(z)가 하이퍼볼릭 탄젠트 함수인 경우, g'(z)는 1 - (g(z))^2로 정의됩니다.
이 식은 (1 - (g(z))^2)로 표현되며, z가 큰 값이면 미분 값은 0에 가깝고, z가 작은 값이면 다시 0에 가까워지며, z가 0에 가까울 때 미분 값은 1에 가깝습니다.
ReLU (Rectified Linear Unit)와 Leaky ReLU 활성화 함수: ReLU와 Leaky ReLU 함수의 미분은 다음과 같이 계산됩니다.
g(z)가 ReLU인 경우, g'(z)는 z가 0보다 작을 때는 0이고, z가 0보다 클 때는 1입니다.
g(z)가 Leaky ReLU인 경우, g'(z)는 z가 0보다 작을 때는 특정한 작은 상수(예: 0.01)이고, z가 0보다 클 때는 1입니다.
ReLU와 Leaky ReLU는 z가 0일 때 미분 값이 정의되지 않지만, 대부분의 구현에서는 z가 0인 경우 미분 값을 0 또는 1로 설정하여 사용합니다.
이러한 미분 계산은 역전파 알고리즘에서 기울기를 계산할 때 사용됩니다. 따라서 신경망 내의 각 활성화 함수의 미분을 계산하여 역전파 알고리즘을 구현할 수 있습니다.
Gradient Descent for Neural Networks

이 비디오에서는 신경망의 역전파 및 경사 하강 구현에 대한 방정식을 제공합니다. 이해를 돕기 위해 요약하면 다음과 같습니다.
신경망의 파라미터: 신경망은 W[1], B[1], W[2], B[2]와 같은 파라미터를 갖습니다. 이러한 파라미터의 차원은 각각 다음과 같습니다:
W[1]: (n[1], n[0])
B[1]: (n[1], 1)
W[2]: (n[2], n[1])
B[2]: (n[2], 1)
비용 함수: 이진 분류 작업을 수행한다고 가정하고, 비용 함수 L을 다음과 같이 정의합니다.
L = (1/M) * Σ(L(y_hat, y))
경사 하강: 파라미터를 업데이트하기 위해 경사 하강을 사용합니다. 역전파 알고리즘을 통해 각 파라미터에 대한 미분을 계산해야 합니다.
dW[1], db[1], dW[2], db[2]를 계산하여 파라미터를 업데이트합니다.
역전파 알고리즘: 역전파 알고리즘을 사용하여 미분 값을 계산합니다.
dZ[2] = A[2] - Y
dW[2] = (1/M) * dZ[2] @ A[1].T
db[2] = (1/M) * np.sum(dZ[2], axis=1, keepdims=True)
dZ[1] = (W[2].T @ dZ[2]) * g[1]'(Z[1])
dW[1] = (1/M) * dZ[1] @ X.T
db[1] = (1/M) * np.sum(dZ[1], axis=1, keepdims=True)
역전파는 경사 하강을 위한 파라미터 업데이트에 필요한 미분을 계산합니다. 역전파 알고리즘은 순전파(전방 전파) 및 역전파(오차 역전파) 단계로 구성됩니다.
Backpropagation Intuition (Optional)
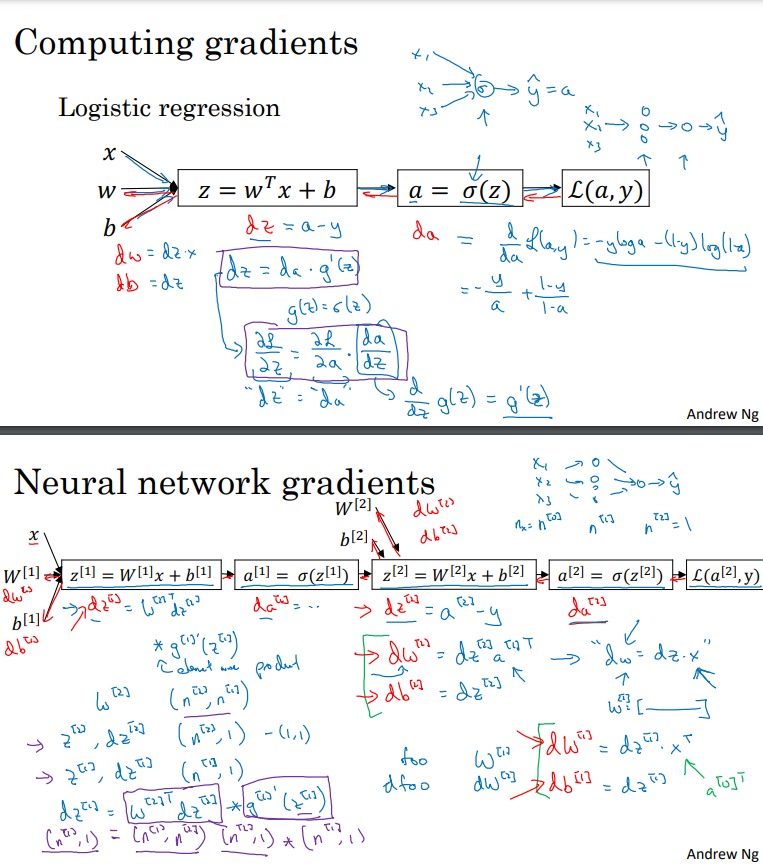
이 동영상에서는 역전파 방정식을 살펴보고 이러한 방정식이 어떻게 유도되었는지에 대한 직관을 얻을 것입니다. .
먼저, 로지스틱 회귀를 다룰 때 순방향과 역방향 단계가 있다는 것을 상기합시다. 로지스틱 회귀의 경우, 손실 함수 L은 다음과 같이 정의되며:
L = -(1/M) * Σ(y * log(a) + (1 - y) * log(1 - a))
이를 미분하여 da를 얻을 수 있습니다. 실제로는 다음과 같습니다:
da = -(y/a - (1 - y)/(1 - a))
da를 구하기 위해 미분을 수행했습니다. 다음으로 dz를 계산할 때는 dz = a - y가 되었습니다. 미분은 계산 방법과 동일한 방식으로 이루어집니다.
다음으로 역전파 알고리즘을 적용할 때, 로지스틱 회귀의 순방향과 역방향 계산을 두 번 수행한다는 것을 상기합시다. 여기에서는 두 개의 레이어로 이루어진 신경망을 다루며, 입력 레이어, 은닉 레이어 및 출력 레이어가 있습니다. 순방향 계산에서는 z1, a1, z2, a2를 계산하고, 이는 z2도 파라미터인 W2와 b2에 의존한다는 점을 주목하세요. 역방향 계산에서는 da2, dz2, dw2, db2를 계산하고, 나중에는 da1, dz1, dw1, db1도 계산해야 합니다.
물론 실제로는 이러한 모든 계산을 벡터화하여 여러 개의 훈련 예제를 처리하게 됩니다. 이를 위해 z, a를 열로 쌓아서 행렬을 만들고 해당 벡터화된 버전으로 역전파 방정식을 계산합니다.

마지막으로, 신경망의 가중치를 무작위로 초기화하는 것이 중요하다는 것을 상기하고, 초기화된 가중치를 사용하여 훈련하는 것이 필요합니다.
이렇게 해서 역전파 알고리즘의 기본 원리를 이해할 수 있게 되었습니다.
Random Initialization
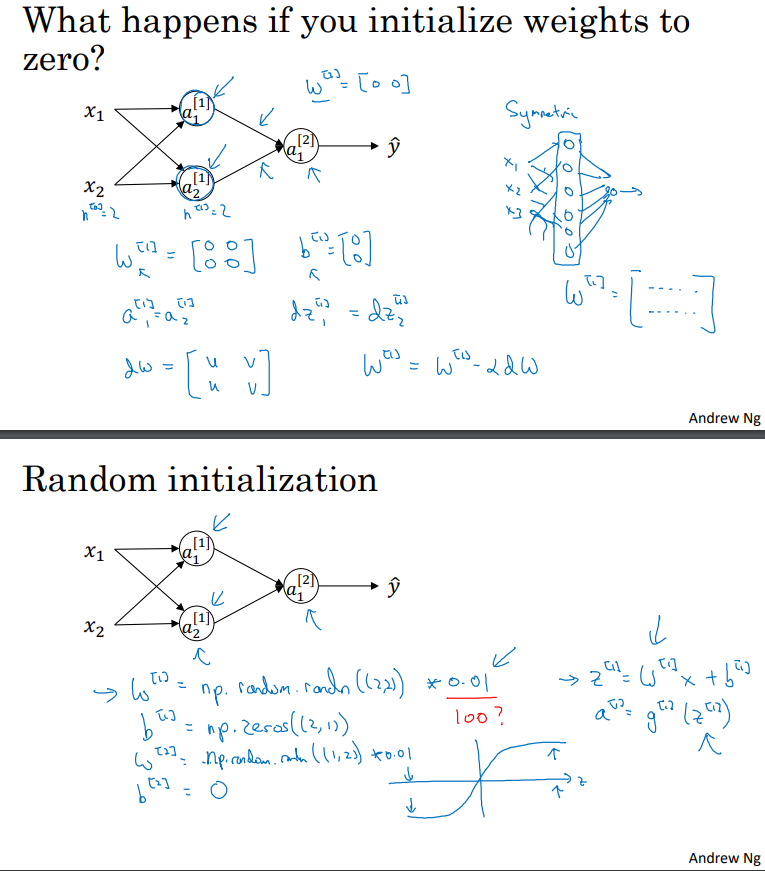
신경망을 변경할 때, 가중치(weights)를 무작위로 초기화하는 것이 중요합니다. 로지스틱 회귀의 경우, 가중치를 0으로 초기화하는 것은 괜찮았지만, 신경망의 경우 가중치를 모두 0으로 초기화하고 그래디언트 따라가기(gradient descent)를 적용하면 제대로 작동하지 않습니다. 이에 대한 이유를 살펴봅시다.
예를 들어, 입력 특성이 2개이고 은닉 유닛이 2개인 경우를 생각해봅시다. 즉, n0 = 2, n1 = 2입니다. 이 경우 은닉 레이어에 해당하는 가중치 행렬 W1은 2x2 행렬이 됩니다. 이 행렬을 모두 0으로 초기화한다고 가정해봅시다. 즉, 다음과 같은 행렬이 됩니다.
0 0
0 0
그리고 B1도 0 0으로 초기화합니다. 이렇게 하면 편향(bias)을 0으로 초기화하는 것은 괜찮지만, 모든 가중치 W를 0으로 초기화하는 것은 문제가 발생합니다. 이런 정식화(포맷)의 문제는 어떤 예제를 주더라도 a1,1과 a1,2가 항상 같아진다는 것입니다. 왜냐하면 두 은닉 유닛이 정확히 같은 함수를 계산하기 때문입니다. 그리고 역전파(backpropagation)를 계산할 때 dz11과 dz12도 대칭성에 따라 항상 같아집니다. 즉, 두 은닉 유닛이 처음에 같은 방식으로 초기화됩니다. 이론적으로, 이렇게 말하면 가중치 행렬의 출력도 동일하게 됩니다. 즉, w2도 다음과 같이 초기화됩니다.
0 0
그러나 신경망을 이렇게 초기화하면 첫 번째 은닉 유닛과 두 번째 은닉 유닛이 완전히 동일한 함수를 계산하게 됩니다. 그리고 이렇게 초기화된 신경망을 학습할 때마다 두 은닉 유닛은 계속해서 동일한 함수를 계산하게 됩니다. 이러한 이유로 두 은닉 유닛이 완전히 동일한 함수를 계산하는 문제가 발생합니다.
이것은 신경망에 여러 개의 은닉 유닛을 둔 이유가 없어지게 되는 문제입니다. 모든 은닉 유닛이 동일한 함수를 계산하므로 의미가 없습니다. 따라서 이 문제를 해결하기 위해 초기 파라미터를 무작위로 설정해야 합니다.
가중치를 무작위로 초기화하는 방법은 다음과 같습니다. 먼저, W1을 다음과 같이 무작위로 초기화합니다.
W1 = np.random.randn(2, 2) * 0.01
여기서 np.random.randn(2, 2)는 평균이 0이고 분산이 1인 가우시안(정규) 분포에서 추출한 난수를 생성하는 함수입니다. 그런 다음, 작은 값을 곱하여 매우 작은 무작위 값으로 초기화합니다. 이것은 일반적으로 가중치를 작은 무작위 값으로 초기화하는 방법 중 하나입니다.
편향(bias) b1은 대칭성 문제가 없으므로 0으로 초기화해도 괜찮습니다.
마찬가지로 W2와 b2도 무작위로 초기화할 수 있습니다.
마지막으로, 초기화에 사용되는 상수 0.01은 어떻게 결정되는지 궁금할 것입니다. 이 값은 일반적으로 매우 작은 값을 선택합니다. 가중치를 너무 크게 초기화하면 활성화 함수(예: 시그모이드 또는 하이퍼볼릭 탄젠트)의 출력이 매우 크거나 작아질 수 있으며, 이로 인해 그래디언트가 매우 작아져서 학습이 느려질 수 있습니다. 따라서 일반적으로 0.01과 같이 작은 값을 선택하는 것이 좋습니다. 딥 러닝 모델을 더 깊게 만들 경우 다른 상수를 선택하는 것이 필요할 수 있으며, 이에 대한 논의는 다음 단계에서 진행될 것입니다.

매개변수 벡터는 열 벡터입니다.
각 레이어의 활성화 기능은 다를 수 있습니다.
Coursera | Online Courses & Credentials From Top Educators. Join for Free | Coursera
Learn online and earn valuable credentials from top universities like Yale, Michigan, Stanford, and leading companies like Google and IBM. Join Coursera for free and transform your career with degrees, certificates, Specializations, & MOOCs in data science
www.coursera.org
