학습 목표
- Explain the convolution operation
- Apply two different types of pooling operations
- Identify the components used in a convolutional neural network (padding, stride, filter, ...) and their purpose
- Build a convolutional neural network
- Implement convolutional and pooling layers in numpy, including forward propagation
- Implement helper functions to use when implementing a TensorFlow model
- Create a mood classifer using the TF Keras Sequential API
- Build a ConvNet to identify sign language digits using the TF Keras Functional API
- Build and train a ConvNet in TensorFlow for a binary classification problem
- Build and train a ConvNet in TensorFlow for a multiclass classification problem
- Explain different use cases for the Sequential and Functional APIs
--------------------------------------------------------------------
CNN의 기본 레이어(풀링, 컨볼루션)를 구현하고 이를 심층 네트워크에 적절히 쌓아 다중 클래스 이미지 분류 문제를 해결합니다.
학습 목표
- 컨볼루션 작동을 설명
- 두 가지 유형의 풀링 작업 적용
- 컨볼루션 신경망에 사용되는 구성 요소(패딩, 스트라이드, 필터 등)와 그 목적을 식별합니다
- 컨볼루션 신경망 구축
- 순방향 전파를 포함하여 컨볼루션 및 풀링 레이어를 numpy로 구현
- TensorFlow 모델 구현 시 사용할 도우미 기능 구현
- TF Keras Sequential API를 사용하여 기분 분류기 생성
- TF Keras Functional API를 사용하여 수화 숫자를 식별하는 ConvNet 구축
- TensorFlow에서 이진 분류 문제에 대한 ConvNet 구축 및 훈련
- 다중 클래스 분류 문제를 위해 TensorFlow에서 ConvNet 구축 및 훈련
- 순차 및 기능성 API의 다양한 사용 사례 설명
Computer Vision
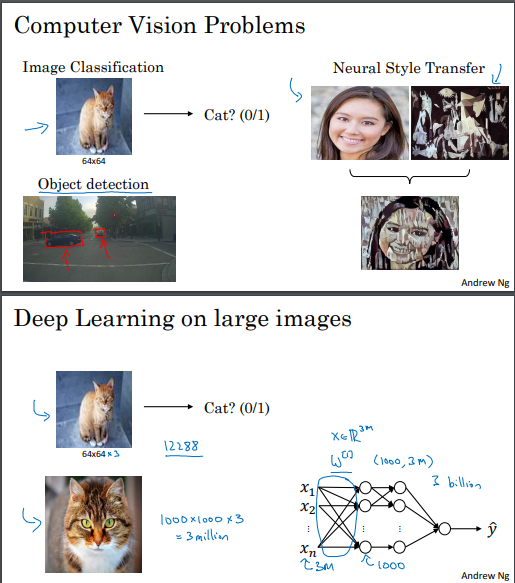
컨볼루션 신경망 (CNN) 소개:
딥러닝을 통한 컴퓨터 비전의 발전이 빠르게 진행되고 있음.
자율 주행 자동차, 얼굴 인식, 음성 인식, 예술 등 다양한 분야에 활용됨.
컴퓨터 비전 문제 예시:
이미지 분류, 물체 탐지, 스타일 전이 등.
문제에 따라 입력 데이터의 크기가 크게 달라짐.
컴퓨터 비전에서의 과제:
입력 데이터가 크고 많은 파라미터를 가진 모델은 과적합 및 계산/메모리 요구사항이 높음.
컨볼루션 연산:
컨볼루션 연산은 CNN의 기본 요소로, 효율적인 이미지 처리를 가능케 함.
에지 검출을 통한 컨볼루션 설명:
에지 검출을 통해 컨볼루션 연산을 설명하고 구현.
Edge Detection Example

수평선 , 수지선 엣지 검출
표기법에 관한 주의사항 중 하나는 수학에서 별표(asterisk) (*)가 컨볼루션을 나타내는 표준 기호이지만, Python에서는 곱셈 또는 요소별 곱셈을 나타내는 데에도 사용된다는 것입니다. 이것은 혼동을 줄 수 있는 부분 중 하나입니다. Python에서는 NumPy나 다른 라이브러리를 사용하여 컨볼루션 연산을 구현할 때 주의해야 합니다.
*컨볼루션은 두 함수 사이의 수학적 연산으로, 한 함수를 다른 함수의 "가중합"으로 변환하는 과정을 나타냅니다.
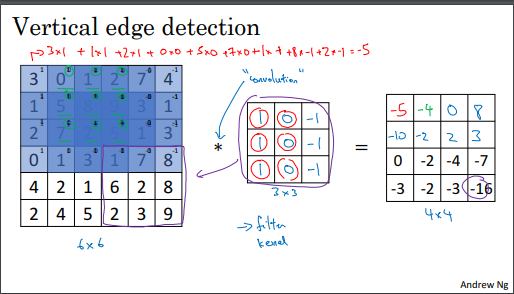
컨볼루션(Convolution) 연산은 컨볼루션 신경망(Convolutional Neural Network, CNN)의 기본 구성 요소 중 하나입니다.
컨볼루션 연산은 이미지 처리에서 에지(Edge) 검출과 같은 작업에 사용됩니다.
에지 검출을 예로 들어 설명하며, 이미지에서 수직 및 수평 에지를 검출하는 방법을 살펴봅니다.
컨볼루션 연산은 이미지와 필터(또는 커널) 간의 가중합과 합성으로 이루어집니다.
컨볼루션 연산의 결과는 입력 이미지를 스캔하여 감지한 특징을 나타내는 새로운 이미지(또는 맵)입니다.
컨볼루션 연산은 미리 정의된 필터를 사용하여 입력 이미지를 스캔하고, 각 위치에서 가중합을 계산하여 특징을 추출합니다.
각 필터는 특정한 패턴 또는 특징을 검출하도록 설계됩니다. 예를 들어, 수직 에지를 검출하는 필터는 왼쪽에서 밝은 부분, 중간에서 어두운 부분, 오른쪽에서 어두운 부분을 구별할 수 있습니다.
More Edge Detection
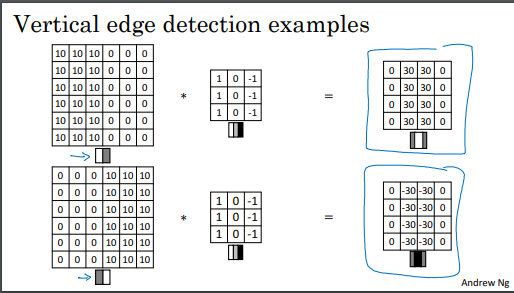
수직 에지 검출:
이전 강의에서 다룬 예시를 다시 살펴봅니다. 왼쪽은 밝고 오른쪽은 어두운 영상에서 컨볼루션 연산을 수행하여 수직 에지를 감지합니다.
색상 반전:
밝음과 어두움의 색상이 반전된 이미지를 고려합니다. 이 경우, 수직 에지 감지 필터를 동일하게 적용하면 결과적으로 음수 값의 에지가 나타납니다. 이는 에지 전환의 색상이 반전되었음을 의미하며, 음수 값은 어둠에서 밝음으로의 에지를 나타냅니다.
에지 종류 구분:
이 필터는 밝음에서 어둠으로의 에지와 어둠에서 밝음으로의 에지를 구별합니다. 따라서 양의 에지와 음의 에지를 구별하는 데 사용됩니다.
절댓값 사용:
양의 에지와 음의 에지 중 어떤 것이든 상관하지 않으려면 출력 행렬의 절댓값을 취할 수 있습니다.

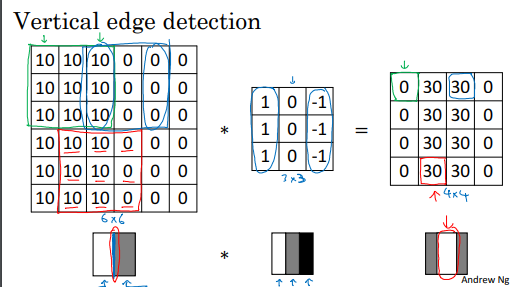
수직 에지 감지:
수직 에지 감지를 위해 사용한 필터에 따라, 밝은 부분은 왼쪽에, 어두운 부분은 오른쪽에 있는 3x3 영역을 수직 에지로 인식합니다.
수평 에지 감지:
비슷하게, 수평 에지는 밝은 부분이 위쪽에, 어두운 부분이 아래 행에 있는 3x3 영역을 수평 에지로 인식합니다.
예제:
좀 더 복잡한 예제를 살펴봅니다. 이 예제에서는 왼쪽 상단과 오른쪽 하단 모서리에 10이 있는 이미지를 고려합니다. 이를 시각화하면 어두운 영역에 0이 있으므로 해당 부분을 어둡게 채우고, 왼쪽 상단과 오른쪽 하단 모서리는 밝게 표시됩니다. 이 이미지를 수평 에지 감지기로 컨볼루션하면 결과는 다음과 같습니다.
결과 분석:
결과 중 30은 밝은 부분이 위쪽에 있고 아래쪽 행에 어두운 픽셀이 있는 3x3 영역을 나타내며, 이는 양의 에지를 나타냅니다.
결과 중 -30은 아래쪽이 더 밝고 위쪽이 어두운 3x3 영역을 나타내며, 이는 음의 에지를 나타냅니다.
작은 이미지에서는 중간값이 나타날 수 있지만 대규모 이미지에서는 중요한 에지가 제대로 표시됩니다.
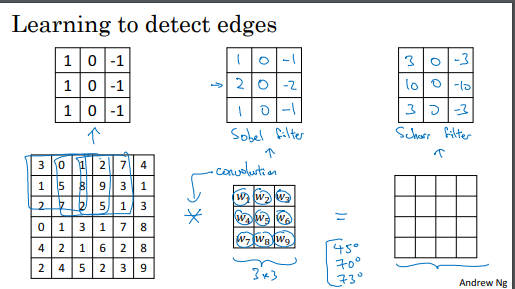
다양한 에지 검출:
3x3 필터를 사용하여 수직 에지 및 수평 에지를 감지할 수 있음.
에지 검출 필터는 밝은 픽셀에서 어두운 픽셀 또는 어두운 픽셀에서 밝은 픽셀로의 에지 전환을 나타낼 수 있음.
수평 에지 감지:
수평 에지는 3x3 영역에서 위쪽이 밝고 아래쪽 행이 어두운 픽셀로 특징화됨.
다양한 필터:
수직 에지 검출 필터 외에도 다른 필터를 사용할 수 있음.
예를 들어, Sobel 필터 및 Scharr 필터는 중앙 픽셀에 가중치를 부여하여 더 견고한 결과를 제공함.
필터 학습:
딥 러닝에서는 필터를 학습하여 데이터의 특징을 더 잘 포착할 수 있음.
백프로파게이션을 사용하여 3x3 필터의 9개 매개변수를 학습함.
이를 통해 신경망은 수직, 수평 에지뿐만 아니라 다른 각도의 에지도 학습할 수 있음.
에지 검출의 핵심:
컨볼루션 연산은 학습된 필터를 이미지의 여러 위치에 적용하여 원하는 특징을 출력함.
파라미터 학습:
필터의 9개 숫자를 학습 가능한 매개변수로 취급하는 아이디어는 컴퓨터 비전에서 가장 강력한 아이디어 중 하나임.
추가 학습:
이러한 매개변수를 학습하는 방법에 대한 자세한 내용은 나중에 다룰 예정임.
Padding
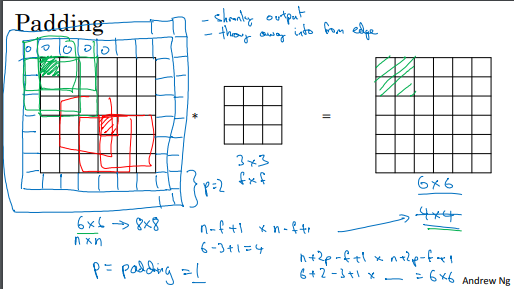
패딩 (Padding):
딥 뉴럴 네트워크를 구축하기 위한 필수적인 컨볼루션 연산의 한 가지 변경 사항은 패딩입니다.
기존에 6x6 이미지를 3x3 필터와 컨볼루션하면 4x4 출력이 되는데, 이는 입력 이미지 크기에서 필터 크기를 뺀 값에 +1을 한 것입니다.
패딩의 필요성:
컨볼루션을 적용할 때마다 이미지 크기가 줄어들어, 심층 신경망에서 이미지가 지나치게 작아지는 문제가 발생합니다.
이미지 가장자리에 위치한 픽셀은 출력에 미치는 영향이 적어 정보 손실이 발생합니다.
패딩을 사용한 해결책:
이미지 주변을 추가 픽셀로 패딩하면 이러한 문제를 해결할 수 있습니다.
일반적으로 0으로 패딩합니다. 패딩의 양을 p라고 하면, 출력은 n+2p-f+1 by n+2p-f+1이 됩니다.
패딩을 적용하면 입력 이미지의 크기를 유지할 수 있으며 가장자리 픽셀의 정보 손실을 줄일 수 있습니다.
패딩의 예:
패딩을 한 예로 p=1로 설정하면 입력 이미지가 6x6에서 8x8로 패딩되며 출력은 여전히 6x6이 됩니다.
필요에 따라 더 많은 픽셀로 패딩할 수 있습니다.
패딩은 딥 뉴럴 네트워크에서 이미지 크기를 유지하고 정보 손실을 방지하는 중요한 기술입니다.

패딩 (Padding)을 사용한 컨볼루션:
패딩을 통해 입력 이미지의 크기를 유지하거나 원하는 출력 크기를 얻을 수 있습니다.
패딩의 양은 주로 p 픽셀로 설정하며, p = (f - 1) / 2 (f는 필터 크기)로 지정하면 출력 크기를 입력과 동일하게 유지할 수 있습니다.
패딩 종류:
"Valid convolution"은 패딩을 적용하지 않고, 출력 크기가 입력보다 작게 됩니다.
"Same convolution"은 패딩을 적용하여 출력 크기를 입력과 동일하게 유지합니다.
컴퓨터 비전에서는 필터 크기 f가 주로 홀수로 사용되며, f가 홀수일 때 Same convolution을 사용하면 좋은 패딩 결과를 얻을 수 있습니다.
홀수 필터 크기의 권장 사용:
컴퓨터 비전에서는 홀수 필터 크기 (3x3, 5x5 등)가 자주 사용됩니다.
홀수 필터 크기는 대칭적인 패딩을 제공하고 중앙 픽셀을 가질 수 있어 필터의 위치를 명확하게 지정할 수 있습니다.
패딩 종류 지정:
컨볼루션 연산에서 패딩을 지정할 때, p 값을 설정하거나 "Valid convolution" 또는 "Same convolution"을 명시할 수 있습니다.
"Valid convolution"은 패딩 없음을 의미하며, "Same convolution"은 필요한 만큼 패딩을 적용하여 출력 크기를 입력과 동일하게 유지합니다.
Strided Convolutions

스트라이드 컨볼루션 (Stride Convolutions):
스트라이드 컨볼루션은 컨볼루션 신경망의 기본 구성 요소 중 하나입니다.
스트라이드는 컨볼루션 연산 시 필터를 이동시키는 간격을 나타냅니다.
스트라이드 컨볼루션 예시:
7x7 이미지를 3x3 필터로 스트라이드 2로 컨볼루션하는 예시를 보여줍니다.
스트라이드가 2인 경우, 필터를 2칸씩 이동시킵니다.
각 위치에서 필터와의 요소별 곱과 합을 계산하여 출력 값을 얻습니다.
입력 및 출력 크기 계산:
입력 이미지 크기가 n x n이고, 필터 크기가 f x f이며, 패딩 p 및 스트라이드 s를 사용하는 경우, 출력 크기는 다음과 같이 계산됩니다:
출력 크기 = (n + 2p - f) / s + 1
소수점 처리:
계산 결과가 소수일 경우 내림(round down)합니다.
내림은 가장 가까운 정수 값으로 반올림하지 않고 내림하는 것을 의미합니다.
출력을 생성하기 위해 필터가 이미지 또는 이미지와 패딩 영역 내에 완전히 포함되어야 합니다.

출력 크기 계산:
입력 이미지 크기(n x n), 필터 크기(f x f), 패딩(p), 스트라이드(s)에 따른 출력 크기는 다음과 같이 계산됩니다:
출력 크기 = (n + 2p - f) / s + 1
소수 처리:
계산 결과가 소수일 경우 내림(round down)합니다.
내림은 가장 가까운 정수 값으로 반올림하지 않고 내림하는 것을 의미합니다.
교차 상관(Cross-Correlation) vs. 합성곱(Convolution):
수학 및 신호 처리 교과서에서 정의된 합성곱은 실제로 필터를 수평 및 수직 축을 기준으로 뒤집는 작업을 포함합니다.
딥 러닝에서는 이 뒤집기 작업을 생략하고, 이를 교차 상관(Cross-Correlation)으로 간주합니다.
딥 러닝 문헌에서는 주로 이를 "합성곱(Convolution)"으로 표기하며, 대부분의 경우 뒤집기를 생략합니다.
뒤집기의 중요성:
뒤집기를 적용하면 합성곱 연산이 결합 법칙(associativity)을 가지며, 이는 신호 처리 응용 분야에 유용합니다.
그러나 딥 러닝에서는 뒤집기를 생략하여도 결과에 영향을 미치지 않으며 코드를 단순화합니다.
Convolutions Over Volume

3D 볼륨에서의 합성곱:
2D 이미지뿐만 아니라 3D 볼륨 상에서 합성곱을 구현할 수 있습니다.
RGB 이미지의 경우, 6x6x3 크기의 이미지는 세 개의 컬러 채널을 가진 스택으로 간주할 수 있습니다.
3D 필터도 마찬가지로 높이, 너비, 채널 수를 갖습니다. 이미지와 필터의 채널 수는 일치해야 합니다.
3D 볼륨 합성곱 연산:
3D 이미지와 3D 필터를 사용하여 합성곱을 수행합니다.
필터를 이미지 상단 좌측에 배치한 다음, 해당 위치에서 각 채널의 값을 곱하고 합산하여 출력을 생성합니다.
필터를 한 칸씩 이동시키면서 다음 출력을 계산하고, 이를 반복하여 출력을 완성합니다.
다양한 특징 감지:
다른 필터를 사용하여 다양한 특징을 감지할 수 있습니다. 예를 들어, 수직 엣지, 수평 엣지, 대각선 엣지, 등을 동시에 감지하는 데 여러 필터를 사용할 수 있습니다.
출력 볼륨:
여러 필터를 사용하면 출력은 각 필터에 해당하는 채널 수를 가지게 됩니다. 따라서 출력은 4x4x2와 같이 볼륨 형태로 구성됩니다.
깊이(Depth)와 채널:
볼륨의 세 번째 차원은 "채널" 또는 "깊이"로 표현됩니다. 이러한 용어는 뒤섞일 수 있으나, 채널 용어가 더 흔하게 사용됩니다.
One Layer of a Convolutional Network

3D 볼륨과 필터:
이전 비디오에서 3D 볼륨을 가지고 두 개의 다른 필터와 합성곱하는 방법을 배웠습니다.
이 예에서는 두 개의 다른 4x4 출력을 얻기 위해 사용됩니다.
필터를 적용하고 편향 추가:
첫 번째 필터로 합성곱을 수행하고 4x4 출력을 생성합니다.
이 출력에는 각 요소에 대한 편향(bias)이 추가됩니다.
그런 다음 비선형 함수(예: ReLU)를 적용하여 최종 4x4 출력을 얻습니다.
두 번째 필터도 동일한 과정을 거쳐 다른 4x4 출력을 생성합니다.
복수의 출력 스택:
두 개의 출력을 스택하여 4x4x2 출력 볼륨을 생성합니다.
이 볼륨의 크기는 필터의 개수에 따라 결정됩니다. (이 예에서는 2개의 필터를 사용하여 2)
비교적 표준 신경망과의 비교:
CNN 계층의 작동 방식을 표준 신경망 계층과 비교합니다.
CNN에서는 합성곱 연산이 선형 연산으로 작용하고, 이에 편향 및 비선형 함수가 적용됩니다.
다수 필터의 경우:
두 개의 필터 대신 10개의 필터를 사용하면 4x4x10 출력 볼륨을 얻을 수 있습니다.
10개의 출력을 쌓아 4x4x10 출력을 형성합니다.

각 필터는 3x3x3 크기의 3D 볼륨입니다. 따라서 각 필터에는 27개의 매개변수가 있습니다.
각 필터에 편향(bias)을 더하면 총 28개의 매개변수가 됩니다.
예를 들어, 두 개의 필터 대신 실제로 10개의 필터가 있다고 상상하면, 매개변수의 총 수는 28 x 10 = 280개가 됩니다.
CNN의 한 가지 장점은 입력 이미지의 크기가 얼마나 크든지 상관없이 매개변수 수가 고정된 280개로 유지된다는 것입니다. 이로써 10개의 필터를 사용하여 대규모 이미지에서도 특징(예: 세로 가장자리, 가로 가장자리 등)을 감지할 수 있습니다.
CNN은 과적합에 민감하지 않아서 10개의 기능 감지기를 학습한 후에 이를 큰 이미지에도 적용할 수 있습니다. 매개변수 수는 여전히 상대적으로 작은 280개입니다.

CNNs (Convolutional Neural Networks)은 대규모 이미지에도 과적합에 취약하지 않은 특성을 가집니다. 이미지 크기가 어떻든지 상관없이 매개변수 수가 상대적으로 작고 고정되어 있기 때문입니다.
각 필터는 3x3x3 크기의 3D 볼륨이며 27개의 매개변수를 가집니다. 편향(bias)을 더하면 총 28개의 매개변수가 됩니다.
필터 수가 10개라면, 총 매개변수 수는 280개가 됩니다. 이것은 CNN의 또 다른 강점 중 하나입니다.
CNN 레이어를 설명하는 표기법: l은 레이어 번호, f[l]은 필터 크기, p[l]은 패딩 양, s[l]은 스트라이드입니다.
입력 크기는 nH[l-1] x nW[l-1] x nC[l-1]로 표시되며, 출력 크기는 nH[l] x nW[l] x nC[l]로 표시됩니다.
필터 크기는 f[l] x f[l] x nC[l-1]이며, 가중치 파라미터 수는 필터 수에 따라 결정됩니다.
편향 파라미터는 각 필터당 하나씩 존재하며, 총 필터 수와 동일한 차원을 가집니다.
변수 순서 표기법: 높이(H), 너비(W), 채널(C) 순서로 표시됩니다.
Simple Convolutional Network Example

강의 오류
*p=0은 same convolutions 대신 valid convolutions을 의미합니다.
패딩을 0으로 설정하면 "valid convolutions"이 발생합니다.
-------------------
이미지 분류 문제를 예로 들어봅시다. 이미지를 입력으로 받고, 그것이 고양이인지 아닌지를 판단하는 문제입니다. 이를 위해 ConvNet 예시를 만들어보겠습니다. 이 예제를 위해 비교적 작은 이미지를 사용하겠습니다. 이미지 크기는 39 x 39 x 3입니다. 이 크기 선택은 몇 가지 수치를 더 나아지게 만드는 데 도움이 됩니다. 따라서 l=0 레이어에서의 nH는 39, nW는 39, 그리고 nc는 3입니다.
첫 번째 레이어는 3 x 3 필터 세트를 사용하여 특징을 감지합니다. 이 필터 크기는 f=3 또는 f[1]=3로 표기하며, 스트라이드는 1이고 패딩은 없습니다. 10개의 필터를 사용한다고 가정하면 다음 레이어의 활성화 크기는 37 x 37 x 10이 됩니다.
다음으로 또 다른 합성곱 레이어를 고려해보겠습니다. 이번에는 5 x 5 필터를 사용하고, 스트라이드는 2로 설정합니다. 패딩은 없으며 20개의 필터를 사용한다고 가정하면, 다음 레이어의 출력은 17 x 17 x 20이 됩니다.
마지막으로 5 x 5 필터와 스트라이드 2를 사용하는 또 다른 합성곱 레이어를 적용하겠습니다. 이로 인해 출력 크기는 7 x 7 x 40이 됩니다. 그런 다음, 일반적으로 이 7 x 7 x 40 크기의 출력을 1,960개의 단위로 펼쳐서 벡터로 만들고, 이를 로지스틱 회귀 또는 소프트맥스 유닛에 공급하여 최종 예측 결과를 얻을 수 있습니다.
일반적으로 ConvNet 예시는 이와 유사할 것입니다. 합성곱 신경망을 설계할 때 많은 작업은 이러한 하이퍼파라미터를 선택하는 것입니다. 출력 크기, 스트라이드, 패딩 및 필터 수를 어떻게 선택할지에 대한 결정이 중요합니다.
전형적인 ConvNet에서 일반적으로 세 가지 종류의 레이어가 있습니다. 하나는 합성곱 레이어이며 Conv 레이어로 표시됩니다. 그리고 아직 보지 않았지만 다음 두 가지 일반적인 레이어가 있습니다. 하나는 풀링 레이어로 Pool이라고 합니다. 그리고 마지막으로 완전 연결 레이어인 FC(Fully Connected)입니다. Conv 레이어만 사용하여 꽤 좋은 신경망을 설계할 수 있지만 대부분의 신경망 구조에는 풀링 레이어와 완전 연결 레이어도 포함됩니다.
다행히 풀링 레이어와 완전 연결 레이어는 합성곱 레이어보다 간단하게 정의됩니다. 나중 비디오에서 더 자세히 설명하겠습니다. 이제 가장 일반적인 ConvNet 레이어 유형을 모두 본 것입니다. 이를 통해 더 강력한 네트워크를 구축할 수 있게 될 것입니다.
Pooling Layers

풀링 레이어란?
풀링 레이어는 주로 표현의 크기를 줄이고 계산 효율성을 높이는 데 사용됩니다. 예를 들어, 최대 풀링(max pooling)이라는 풀링 방식을 살펴보겠습니다. 최대 풀링을 적용할 때, 4x4 크기의 입력이 2x2 크기의 출력으로 바뀝니다.
최대 풀링 동작 방식
4x4 입력을 여러 영역으로 나누고, 각 영역에서 가장 큰 값을 선택하여 출력으로 사용합니다. 이것을 통해 4x4 입력이 2x2 출력으로 줄어듭니다. 이러한 최대 풀링에서 사용되는 두 가지 중요한 하이퍼파라미터는 필터 크기(f)와 스트라이드(s)입니다. 여기서는 2x2 크기의 필터(f=2)와 스트라이드 2(s=2)를 사용한 예시입니다.
최대 풀링의 핵심 아이디어
최대 풀링의 핵심 아이디어는 특정 영역에서 어떤 기능이 감지되면 해당 영역에서 가장 큰 값을 유지하고, 기능이 감지되지 않으면 해당 영역에서 가장 큰 값이 여전히 작다는 것입니다. 이것은 풀링 레이어를 통해 주요 기능을 강조하고 작은 세부 특징을 무시하는 효과가 있습니다.
최대 풀링의 장점
최대 풀링은 실험적으로 잘 작동하는 것으로 알려져 있으며, 주요 하이퍼파라미터(f와 s)를 설정한 후에는 학습할 매개변수가 없어 간단하게 구현할 수 있습니다.
풀링 레이어의 목적은 특징을 더 작은 공간으로 압축하여 계산 효율성을 향상시키고, 더 강력한 특징을 추출하는 것입니다. 최대 풀링은 주요 특징을 보존하면서 크기를 줄이는 데 도움이 됩니다.
------------------------------------------------------------------------------------
Max Pooling 동작 예시: Max Pooling은 주로 풀링 레이어에서 사용되며, 입력 데이터의 크기를 줄이는 데 쓰입니다. 예시로 5x5 크기의 입력 데이터를 사용하고, 3x3 크기의 필터로 Max Pooling을 수행하는 상황을 살펴보겠습니다.
하이퍼파라미터 설정: 필터 크기(f)는 3x3이며, 스트라이드(s)는 1로 설정합니다. 이러한 하이퍼파라미터로 인해 출력 크기는 3x3이 됩니다.
Max Pooling 계산: Max Pooling은 주어진 영역에서 가장 큰 값을 선택하는 연산입니다. 이 예시에서는 각 출력 요소를 계산하는 과정을 설명합니다.
상단 좌측: 3x3 영역에서 최대값 9을 선택합니다.
상단 우측: 3x3 영역에서 최대값 5를 선택합니다.
중단 좌측: 3x3 영역에서 최대값 9를 선택합니다.
중단 우측: 3x3 영역에서 최대값 5를 선택합니다.
하단 좌측: 3x3 영역에서 최대값 8을 선택합니다.
하단 우측: 3x3 영역에서 최대값 9를 선택합니다.
3D 입력에 대한 Max Pooling: 만약 3D 입력 데이터가 있다면, 출력 크기는 동일한 차원을 유지합니다. 예를 들어, 5x5x2 크기의 입력은 3x3x2 크기의 출력을 생성하며, 각 채널에 대해 독립적으로 Max Pooling이 수행됩니다.
Max Pooling의 특징: Max Pooling은 입력 데이터를 각 채널별로 독립적으로 처리하며, 주요 특징을 보존하면서 데이터 크기를 줄이는 데 사용됩니다.
Max Pooling은 특징을 압축하고 계산 효율성을 높이는 데에 사용되며, 각 채널에 대해 독립적으로 동작하므로 쉽게 구현할 수 있습니다.

Average Pooling: Average Pooling은 매우 자주 사용되지는 않지만 간단히 언급됩니다. Max Pooling이 가장 큰 값을 선택하는 것과 달리, Average Pooling은 각 필터 내에서 평균값을 취합니다. 예를 들어, 주어진 예시에서는 하이퍼파라미터로 f(필터 크기)가 2이고 s(스트라이드)가 2인 경우를 보여줍니다. 보통은 Max Pooling이 Average Pooling보다 더 많이 사용됩니다.
Pooling 하이퍼파라미터: Pooling 레이어의 하이퍼파라미터로는 필터 크기(f)와 스트라이드(s)가 있습니다. 일반적으로 사용되는 하이퍼파라미터로는 f=2, s=2가 있으며, 이 설정은 표현의 높이와 너비를 대략적으로 2배로 줄입니다.
패딩: 대부분의 경우, 풀링 레이어에서는 패딩을 사용하지 않습니다. p(패딩) 하이퍼파라미터는 거의 사용되지 않으며, 대부분의 경우 p=0으로 설정됩니다.
풀링의 특징: 풀링 레이어는 학습해야 할 매개변수가 없는 고정된 함수입니다. 역전파(backpropagation)를 통해 조정되는 매개변수가 없으며, 하이퍼파라미터는 한 번 설정하면 고정됩니다.
풀링은 입력 데이터의 공간적 크기를 줄이고 계산 효율성을 높이는 데 사용되며, 주로 Max Pooling이 많이 사용됩니다.
CNN Example

CNN 구성 요소: CNN을 구성하는 주요 구성 요소에는 합성곱층(Convolutional Layer), 풀링층(Pooling Layer), 완전 연결층(Fully Connected Layer), 그리고 소프트맥스(Softmax) 층이 있습니다.
예시 모델: 예시로 32 x 32 x 3(RGB 이미지)를 입력으로 하는 CNN 모델을 살펴봅니다. 이 모델은 LeNet-5에서 영감을 받았으며 여러 하이퍼파라미터를 선택해 구성됩니다.
합성곱층(Conv Layer):
첫 번째 레이어는 5 x 5 필터, 스트라이드 1, 패딩 없음으로 구성됩니다.
출력 크기: 28 x 28 x 6
Conv 1 레이어로 표시하며, Conv 1과 Pool 1은 하나의 레이어로 취급됩니다.
풀링층(Pooling Layer):
첫 번째 풀링 레이어는 2 x 2 Max Pooling을 사용하며, 스트라이드 2를 적용합니다.
출력 크기: 14 x 14 x 6
Pool 1 레이어로 표시하며, Layer 1에 속합니다.
추가 Conv 레이어:
다음으로 5 x 5 필터, 스트라이드 1, 10개의 필터를 사용하는 Conv 2 레이어를 적용합니다.
출력 크기: 10 x 10 x 10
추가 Max Pooling:
두 번째 풀링 레이어는 2 x 2 Max Pooling을 사용하며, 스트라이드 2를 적용합니다.
출력 크기: 5 x 5 x 10
Pool 2 레이어로 표시하며, Layer 2에 속합니다.
완전 연결층(Fully Connected Layer):
Pool 2의 출력을 400 x 1 차원 벡터로 변환합니다.
FC3는 400개의 입력과 120개의 출력 노드로 구성됩니다.
FC4는 120개의 입력과 84개의 출력 노드로 구성됩니다.
출력 층(Softmax):
최종 출력 레이어로 84개의 입력을 받아 10개의 클래스(숫자 0에서 9까지)를 분류하는 Softmax 층을 적용합니다.
하이퍼파라미터 선택: CNN의 하이퍼파라미터 선택은 중요하며, 다른 연구나 논문에서 효과적으로 작동한 설정을 참고하여 선택하는 것이 좋습니다.
네트워크 구조: 일반적으로 CNN은 합성곱층과 풀링층을 번갈아 가며 사용하고, 마지막에 완전 연결층과 Softmax 층을 두는 패턴을 따릅니다.

Why Convolutions?

합성곱층(Convolutional Layer)의 중요성:
합성곱층(Convolutional Layer)은 신경망에 포함되었을 때 왜 유용한지에 대한 설명이 주어집니다.
합성곱의 두 가지 주요 장점:
합성곱층의 주요 이점으로 "파라미터 공유(Parameter Sharing)"과 "연결의 희소성(Sparsity of Connections)"을 언급합니다.
예시를 통한 설명:
예시로 32 x 32 x 3 차원 이미지와 5 x 5 필터 6개를 사용하는 상황을 들어 설명합니다.
이 경우, fully connected layer를 사용하면 매우 많은 파라미터(14 백만 개)가 필요하게 되는데, 이는 학습에 많은 계산 리소스를 요구하며 모델을 과적합할 위험성이 있습니다.
파라미터의 효율성:
합성곱층에서는 파라미터가 필터당 26개(25개의 가중치 + 1개의 편향)로 제한되므로 효율적인 모델 파라미터 관리가 가능합니다.


파라미터 공유(Parameter Sharing):
파라미터 공유는 특징 검출기(예: 수직 에지 검출기)가 이미지 한 부분에서 유용하다면 다른 부분에서도 유용할 가능성이 높다는 관찰에서 비롯됩니다.
파라미터 공유를 통해 하나의 특징 검출기를 여러 위치에서 재사용할 수 있으므로 파라미터 수가 줄어듭니다.
연결의 희소성(Sparsity of Connections):
합성곱 연산은 입력 그리드 내 작은 부분에만 영향을 미치므로 연결이 희소합니다.
각 출력 유닛은 해당하는 작은 입력 영역과만 연결되며, 다른 픽셀 값은 해당 출력에 영향을 미치지 않습니다.
번역 불변성(Translation Invariance):
합성곱 구조는 이미지가 조금 이동하더라도 비슷한 특징을 캡처하고 동일한 레이블을 할당하는 데 도움이 됩니다.
이러한 특성은 합성곱 신경망이 이미지에서 번역 불변성을 자동으로 학습하고 이를 유용하게 활용할 수 있도록 도와줍니다.
파라미터 수의 효율성:
합성곱 신경망은 작은 파라미터 수로 구성되어 있으므로 효율적인 모델 관리가 가능하며 과적합 위험이 낮습니다.
이 강의는 파라미터 공유와 연결의 희소성을 통해 합성곱 신경망(ConvNet)이 작은 파라미터 수로 효과적으로 동작하며, 이미지 처리와 컴퓨터 비전 분야에서 뛰어난 결과를 얻는 이유를 설명하고 있습니다.

- 컨볼루션(Convolution) 및 합성곱 신경망(ConvNet)이 컴퓨터 비전 분야에서 효과적으로 작동하는 이유에 대한 두 가지 핵심 이점:
- 파라미터 공유(Parameter Sharing): 특징 검출기는 이미지의 여러 부분에서 재사용 가능하며 이로 인해 파라미터 수가 감소합니다.
- 연결의 희소성(Sparsity of Connections): 각 출력 유닛은 입력의 일부만 고려하므로 연결이 희소하며 이로 인해 파라미터 수가 감소합니다.
- 합성곱 신경망은 작은 파라미터 수로 효율적으로 동작하며, 이미지 처리 및 번역 불변성(Translation Invariance) 특성을 활용하여 이미지 인식 작업에서 뛰어난 결과를 얻을 수 있습니다.
- 합성곱 신경망의 구조와 파라미터를 최적화하기 위해 경사 하강법(Gradient Descent) 또는 다른 최적화 알고리즘을 사용하여 비용 함수를 최소화하여 네트워크를 학습할 수 있습니다.
- 학습된 합성곱 신경망은 이미지 분류 작업 및 다른 객체 감지 작업을 수행할 수 있으며 효과적인 모델을 구축하는 데 사용될 수 있습니다.



